Предмет: Математика,
автор: Иван199928
99 БАЛЛОВ. Вычислить интеграл, ПОДРОБНО!!!!!!!
Приложения:
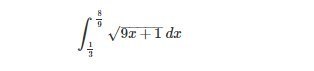
Ответы
Автор ответа:
1
Автор ответа:
1
На картинке ответ.
_______________
_______________
Приложения:
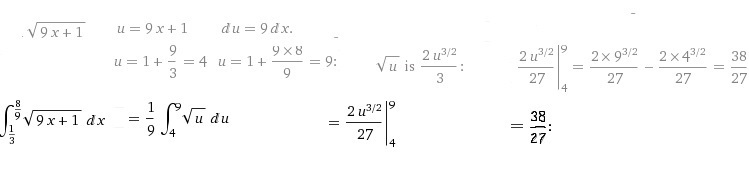
Похожие вопросы
Предмет: Українська мова,
автор: sofiaparhuta6
Предмет: Химия,
автор: dimakosik2008
Предмет: Алгебра,
автор: Sonderese
Предмет: История,
автор: nastya39366
Предмет: Литература,
автор: hivlad17