Предмет: Алгебра,
автор: makapukaaa
Решите 3 любых пожалуйста!
Приложения:
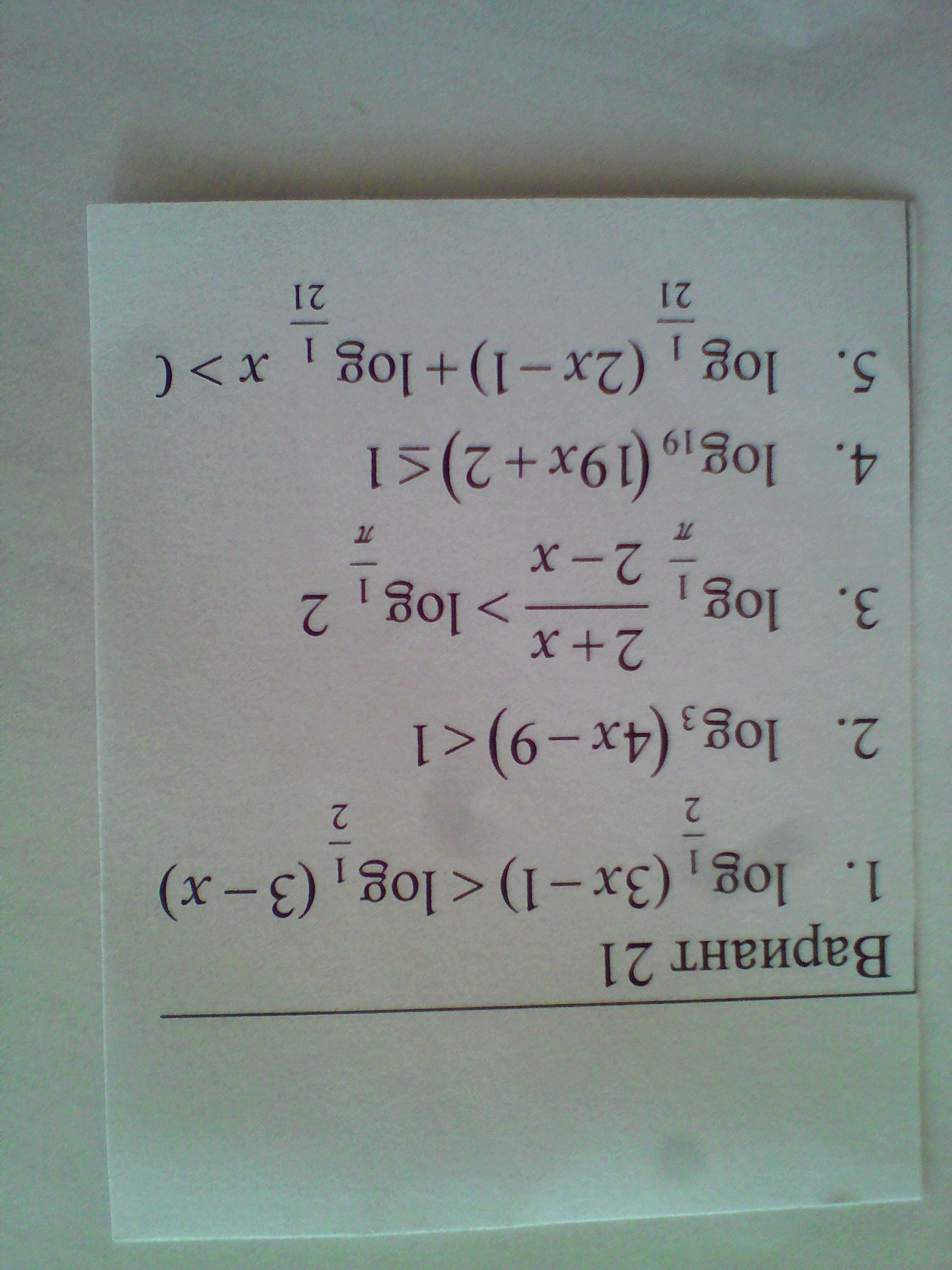
Ответы
Автор ответа:
0
1. Основания логарифмов равны, но они меньше 1, следовательно, знак неравенства меняем на противоположный: 3x-1 > 3-x; x>1
Определяем область допустимых значений
3x-1>0; x>1/3
3-x>0; x<3
Объединяя три последних неравенства, получаем окончательный результат: 1 < x < 3
2. Единицу представляем как 1 = log3(3)
Имеем: log3(4x-9)<log3(3)
Основания логарифмов равны, и они больше 1 - знак неравенства не меняем: 4x-9 < 3; 4x < 12; x <3
Область допустимых значений: 4x-9>0; x>9/4
С учётом последнего 9/4 < x < 3
4. Единицу представляем как 1 = log19(19)
log19(19x+2)=<log19(19)
19x+2=<19; x=<17/19
ОДЗ: 19x+2>0; x>-2/19
Итого: -2/19 < x < 17/19
Определяем область допустимых значений
3x-1>0; x>1/3
3-x>0; x<3
Объединяя три последних неравенства, получаем окончательный результат: 1 < x < 3
2. Единицу представляем как 1 = log3(3)
Имеем: log3(4x-9)<log3(3)
Основания логарифмов равны, и они больше 1 - знак неравенства не меняем: 4x-9 < 3; 4x < 12; x <3
Область допустимых значений: 4x-9>0; x>9/4
С учётом последнего 9/4 < x < 3
4. Единицу представляем как 1 = log19(19)
log19(19x+2)=<log19(19)
19x+2=<19; x=<17/19
ОДЗ: 19x+2>0; x>-2/19
Итого: -2/19 < x < 17/19
Похожие вопросы
Предмет: Литература,
автор: Limon4ek48i
Предмет: ОБЖ,
автор: svitlanachernenko01
Предмет: Математика,
автор: sabraevasabina8
Предмет: Математика,
автор: rogosergh