Предмет: Геометрия,
автор: бесюшка
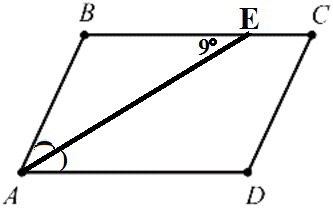
11 Найдите величину острого угла параллелограмма ABCD, если биссектриса угла А образует со стороной ВС угол, равный 9°. Ответ дайте в градусах.
Ответы
Автор ответа:
9
Сумма углов треугольника равна 180°
Из треугольника ABE:
∠B = 180 - 9 - ∠BAE
Сумма соседних углов параллелограмма равна 180°
Из параллелограмма ABCD:
∠B = 180 - 2 * ∠BAE (т.к. биссектриса AE делит угол А пополам)
180 - 9 - ∠BAE = 180 - 2 * ∠BAE
- ∠BAE + 2 * ∠BAE = 180 - 180 + 9
∠BAE = 9 (°)
∠BAD = 9 * 2 = 18 (°)
Из треугольника ABE:
∠B = 180 - 9 - ∠BAE
Сумма соседних углов параллелограмма равна 180°
Из параллелограмма ABCD:
∠B = 180 - 2 * ∠BAE (т.к. биссектриса AE делит угол А пополам)
180 - 9 - ∠BAE = 180 - 2 * ∠BAE
- ∠BAE + 2 * ∠BAE = 180 - 180 + 9
∠BAE = 9 (°)
∠BAD = 9 * 2 = 18 (°)
Приложения:
Похожие вопросы
Предмет: История,
автор: comfypavl9103
Предмет: Алгебра,
автор: chaeririon
Предмет: Английский язык,
автор: fojk95946
Предмет: Химия,
автор: hamnasto