Предмет: Геометрия,
автор: Zhornik2018
Вписанный угол измеряется половиной дуги, на которую он опирается. Покажите наглядно, как это свойство работает.
Ответы
Автор ответа:
4
Есть три варианта расположения центрального угла относительно вписанного:
1) Центр окружности расположен внутри вписанного угла
2) Центр окружности расположен вне вписанного угла
3) Сторона вписанного угла совпадает с диаметром окружности.
Все три доказываются одинаково
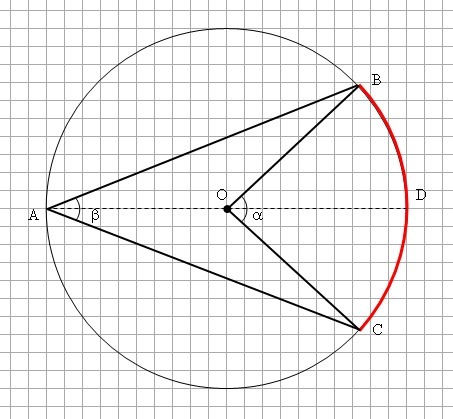
Рассмотрим первый случай.
ΔAOB - равнобедренный, т.к. ОА и ОВ - радиусы окружности
Значит, ∠ВАО=∠АВО.
∠ВОD - внешний для угла ∠ВОА => ∠BOD=∠BAO+∠ABO = 2*∠BAO
То же самое для ΔАОС:
∠DOC=2*∠OAC
Так как ∠ВАС=∠ВАО+∠ОАС и ∠BOC=∠BOD+∠DOC => ∠BOC=2*∠BAC
1) Центр окружности расположен внутри вписанного угла
2) Центр окружности расположен вне вписанного угла
3) Сторона вписанного угла совпадает с диаметром окружности.
Все три доказываются одинаково
Рассмотрим первый случай.
ΔAOB - равнобедренный, т.к. ОА и ОВ - радиусы окружности
Значит, ∠ВАО=∠АВО.
∠ВОD - внешний для угла ∠ВОА => ∠BOD=∠BAO+∠ABO = 2*∠BAO
То же самое для ΔАОС:
∠DOC=2*∠OAC
Так как ∠ВАС=∠ВАО+∠ОАС и ∠BOC=∠BOD+∠DOC => ∠BOC=2*∠BAC
Приложения:
Zhornik2018:
Прошу прощения, можете найти и решить задачу 9-о класса, чтобы в этой задаче применялось свойство?
Я хочу видеть применение данного свойства на практике.
Похожие вопросы
Предмет: Геометрия,
автор: pershikl2000
Предмет: Русский язык,
автор: isan16061982
Предмет: География,
автор: natibunyak34
Предмет: Русский язык,
автор: alina2008lili
Предмет: Математика,
автор: jadira241086