Предмет: Алгебра,
автор: pidenkosergey
если что, ответ =0. Решаю, а получается -1
Приложения:

Ответы
Автор ответа:
0
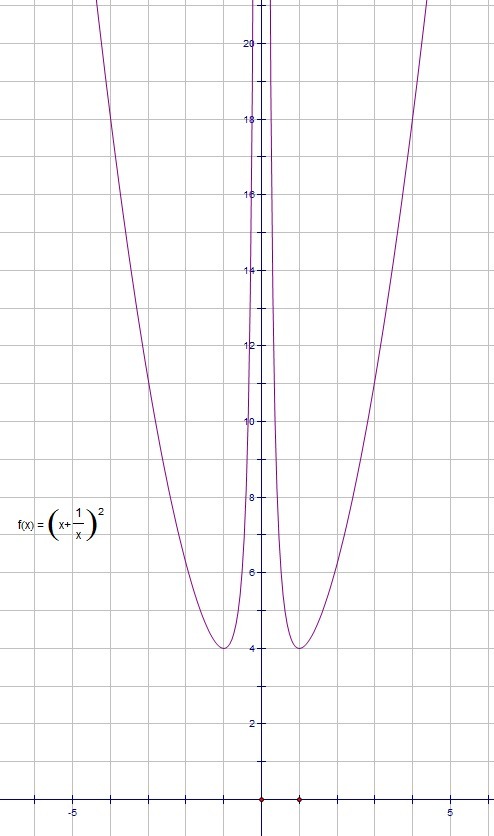
Наименьшее значение функции  равно 4. Она не может принимать значение равное трем
равно 4. Она не может принимать значение равное трем

Противоречие
Противоречие
Приложения:
pidenkosergey:
если ты раскрываешь скобки, то 3 остается
а ты возводишь в квадрат, так делать нельзя
e;t gjyzkf
уже поняла
Похожие вопросы
Предмет: Геометрия,
автор: zhsaule819
Предмет: Другие предметы,
автор: roevakarina866
Предмет: Українська мова,
автор: Аноним
Предмет: Геометрия,
автор: Mariana1123
Предмет: Математика,
автор: markysaborovichok