Предмет: Математика,
автор: igorkuznetsov9
Решите, пожалуйста, очень надо.
Приложения:
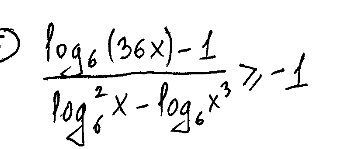
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: История,
автор: makardenlen111
Предмет: Математика,
автор: 20reliance00
Предмет: Другие предметы,
автор: ekaterinaermakova099
Предмет: Математика,
автор: sidorovkirill561
Предмет: Русский язык,
автор: Luns06