Предмет: Математика,
автор: Didicha
Помогите, пожалуйста, решить, очень срочно нужно
Приложения:
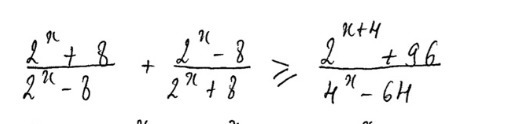
Ответы
Автор ответа:
1
ОГРАНИЧЕНИЯ: 
очевидная замена переменной: , причём
, причём 

обратная замена:

ответ: x∈(3; +∞)
очевидная замена переменной:
обратная замена:
ответ: x∈(3; +∞)
Похожие вопросы
Предмет: Биология,
автор: obemes02
Предмет: Математика,
автор: nkqhzs92fs
Предмет: Литература,
автор: darinamosijcuk95
Предмет: Другие предметы,
автор: Rim2010
Предмет: Математика,
автор: pahsakrot2134