Предмет: Математика,
автор: 31510200
3 примера , очень срочно надо ! 100 балов
Приложения:

Ответы
Автор ответа:
0
третье задание:
1. ответ: x∈[–1,5; +∞)

2. ответ: x∈(–∞; –3]

четвёртое задание:
1. ответ: x∈( ; +∞)
; +∞)

2. ответ: x∈(–∞; 0,8]

3. ответ: x∈(–∞; )
)

1. ответ: x∈[–1,5; +∞)
2. ответ: x∈(–∞; –3]
четвёртое задание:
1. ответ: x∈(
2. ответ: x∈(–∞; 0,8]
3. ответ: x∈(–∞;
Автор ответа:
0
opredelyaem oblast opredeleniya i reshaem neravenstvo
Приложения:
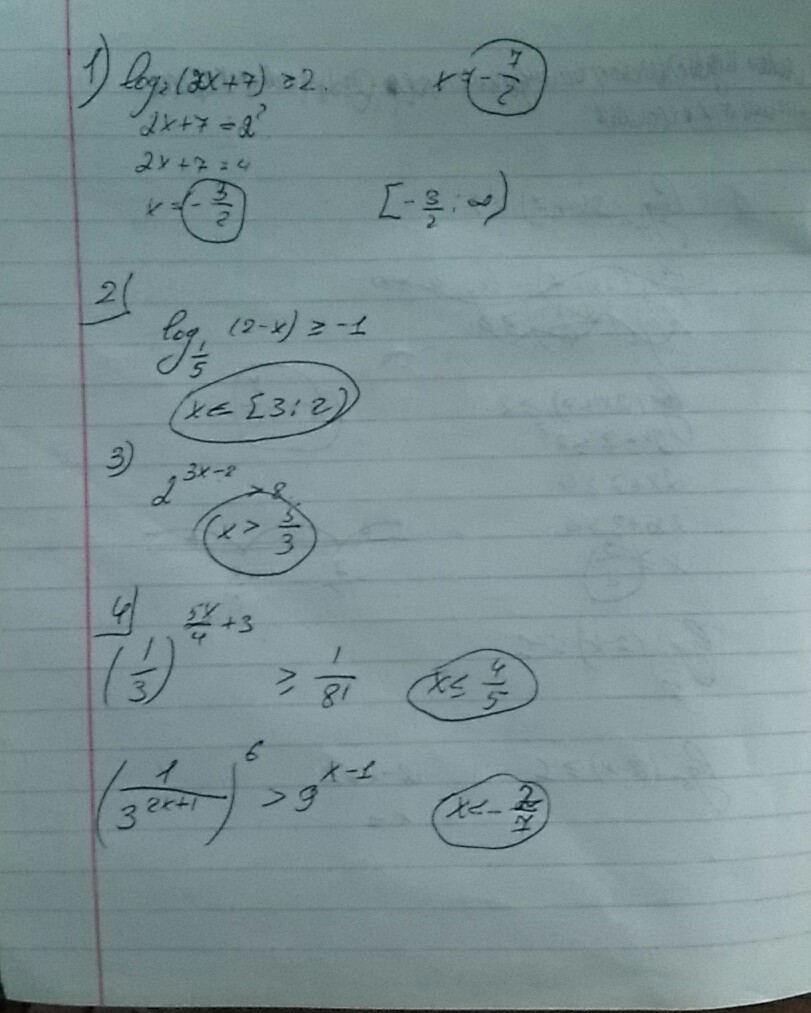
Похожие вопросы
Предмет: Беларуская мова,
автор: b1rd
Предмет: Информатика,
автор: Ggtuq
Предмет: Математика,
автор: vika2001net
Предмет: География,
автор: iop1o
Предмет: Геометрия,
автор: mahmutovaruzana