Предмет: Алгебра,
автор: nyashkoo
решите пожалуйста неравенство
Приложения:
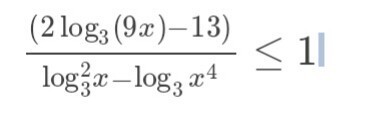
Ответы
Автор ответа:
0
Автор ответа:
0
ОГРАНИЧЕНИЯ: 
очевидная замена :
:

обратная замена:

ответ: x∈(0; 1)∪(81; +∞)
очевидная замена
обратная замена:
ответ: x∈(0; 1)∪(81; +∞)
Похожие вопросы
Предмет: Информатика,
автор: Ggtuq
Предмет: Математика,
автор: vika2001net
Предмет: Английский язык,
автор: mariana5628
Предмет: Геометрия,
автор: mahmutovaruzana
Предмет: Математика,
автор: 12345678965881