Предмет: Математика,
автор: vagjan
ОЧЕНЬ СРОЧНО!!! НОЧЬЮ ПРОСТО РЕШИТЬ НОРМАЛЬНО НЕ МОГУ
Приложения:
Ответы
Автор ответа:
0
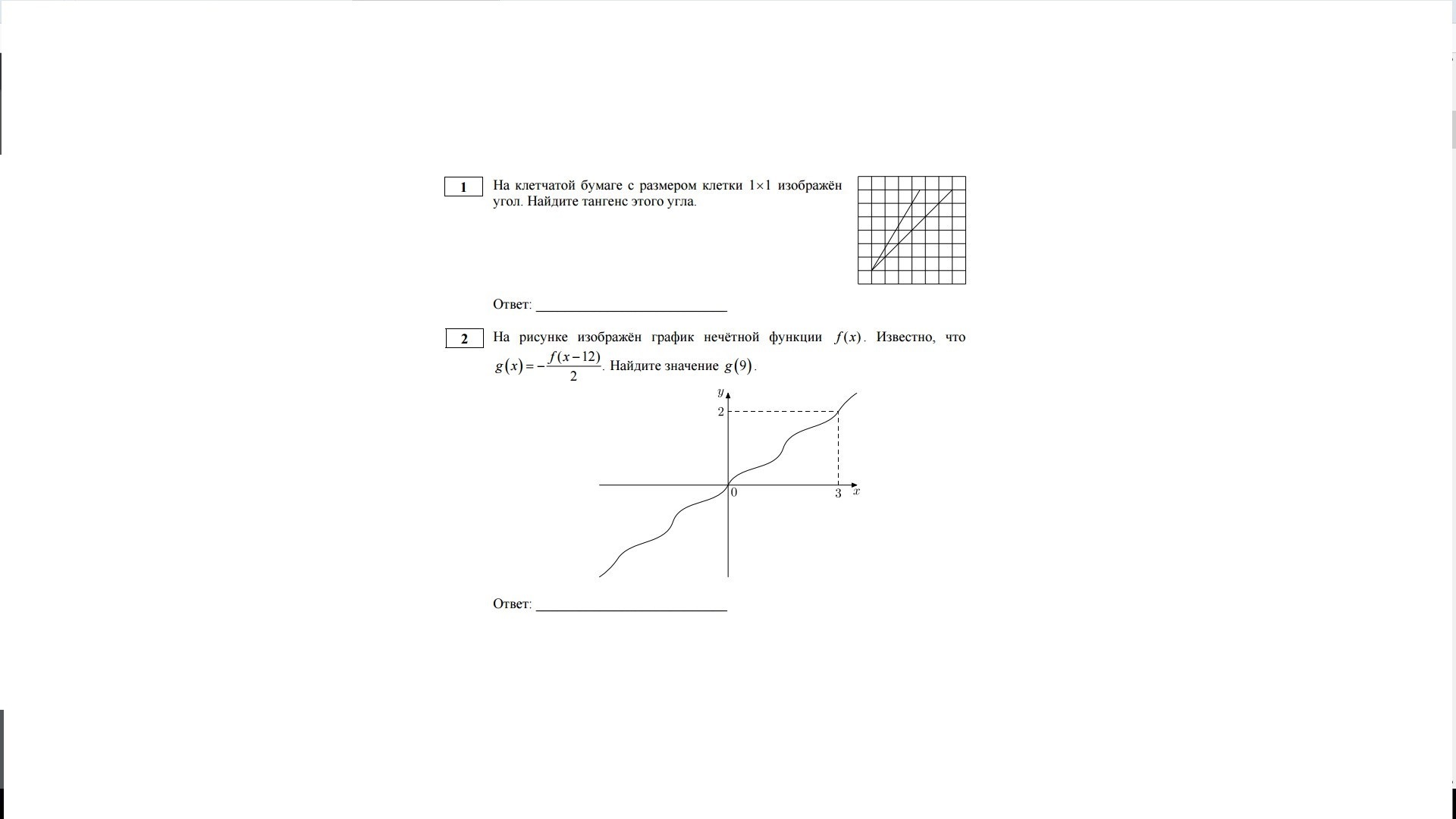
Вариант 1:

Вариант 2:


Вариант 2:
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: artekkracvuk
Предмет: Другие предметы,
автор: aniytkaa9
Предмет: Алгебра,
автор: zubkovaveronikavolod
Предмет: Русский язык,
автор: zoyadavi
Предмет: Русский язык,
автор: dwciaek744