Предмет: Алгебра,
автор: Аноним
Исследовать на сходимость ряд
Приложения:
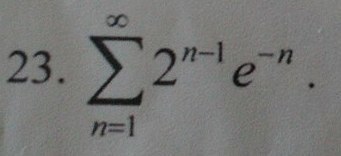
Ответы
Автор ответа:
0
Сходимость ряда определена по признаку Даламбера.
Признак Даламбера: . Если существует предел отношения последующего члена к предыдущему: , то:
а) При q<1 ряд сходится.
б) При q>=1 ряд расходится.
в) При q=1 признак не дает ответа. Нужно использовать другой признак.
2e>1 следовательно ряд расходится
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: efremovaalina799
Предмет: Математика,
автор: Springtrapfnaf123456
Предмет: Математика,
автор: tatiana1286