Question

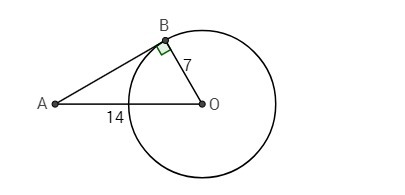
окружность с центром о ав касательная в точка касания ов радиус ао = 14 ов = 7. найти угол а. угол аоб и ав

Answer 1

Радиус, проведенный в точку касания, перпендикулярен касательной, значит ΔАОВ - прямоугольный, ∠В = 90°.

sinA = BO/AO = 7/14 = 1/2   ⇒  ∠A = 30°

∠АОВ = 90°-∠А = 90° - 30° = 60°

По теореме Пифагора:
АВ = √(АО²-ОВ²) = √(14²-7²) = √147 = 7√3