Предмет: Математика,
автор: fugasta
Математика, найти первообразные
Приложения:
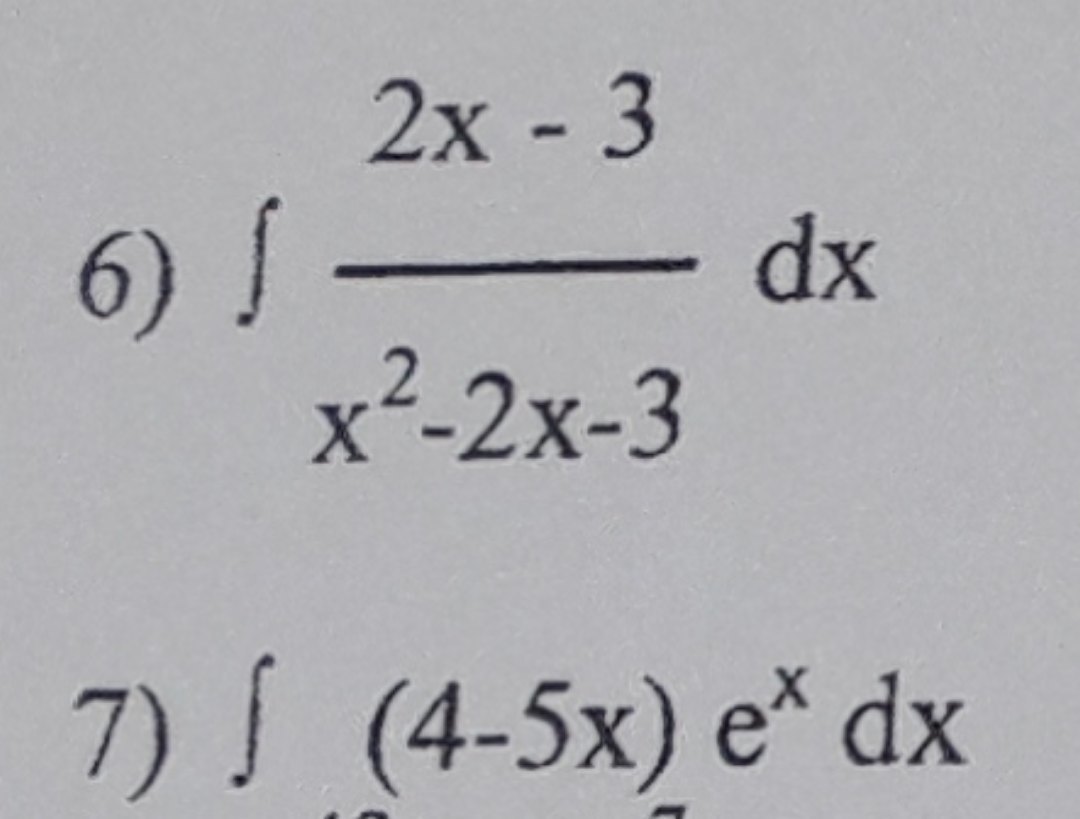
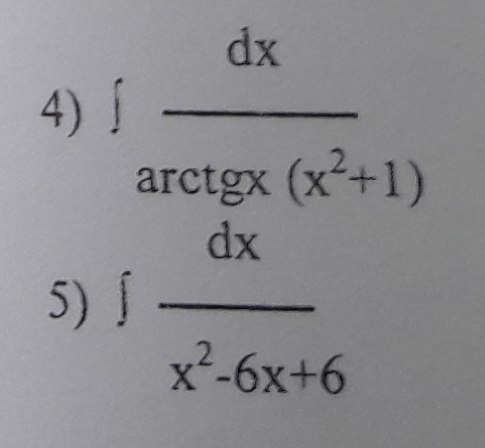
Ответы
Автор ответа:
0
Автор ответа:
0
Во 2 примере надо: (x-3)^2-3 , вместо (х-3)^2+3
Похожие вопросы
Предмет: Английский язык,
автор: keuuahik
Предмет: Русский язык,
автор: kovalevskalana18
Предмет: Математика,
автор: zhusupov339
Предмет: Физика,
автор: alenamelnik69