Предмет: Математика,
автор: qwe123rty456
Равносильны ли уравнения: 2x=x+2 и (2x)^2=(x+2)^2
Решите квадратное уравнение: (2x+3)^2-(x-2)^2=5
Приложения:
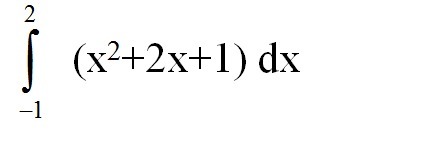
Ответы
Автор ответа:
0
2x=x+2 и (2x)^2=(x+2)^2
2x=x+2 и 4x^2=x^2+4+4x
2x=x+2 и 3x^2=4+4x
Равенства не равносильны.
(2x+3)^2-(x-2)^2=5
4x^2+9+12x=5+x^2+4-4x
4x^2+9+12x-5-x^2-4+4x=0
3x^2+16x=0
x(3x+16)=0
x=0 и 3x+16=0
_____3x=-16
_____x=-16/3
Интеграл на картинке.
2x=x+2 и 4x^2=x^2+4+4x
2x=x+2 и 3x^2=4+4x
Равенства не равносильны.
(2x+3)^2-(x-2)^2=5
4x^2+9+12x=5+x^2+4-4x
4x^2+9+12x-5-x^2-4+4x=0
3x^2+16x=0
x(3x+16)=0
x=0 и 3x+16=0
_____3x=-16
_____x=-16/3
Интеграл на картинке.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: milanaleonidovna1306
Предмет: Алгебра,
автор: anna653460
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: frozenelizaveta