Предмет: Алгебра,
автор: VSIIVIVN
Производная функции.
Приложения:
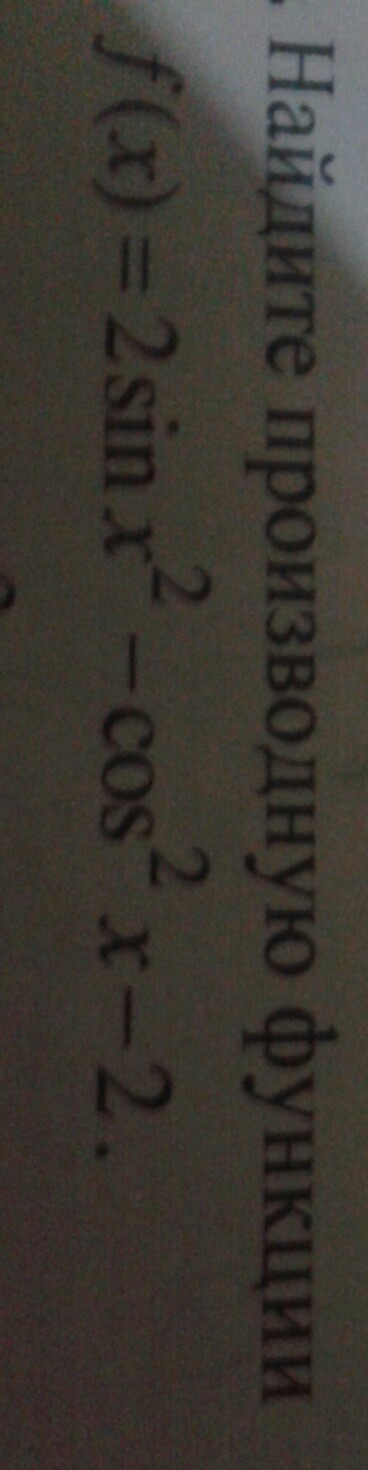
Ответы
Автор ответа:
0
f(x)=2sinx²-cos²x-2
f´(x)=2cosx² . 2x -2cosx.(-sinx)=4xcosx²+2cosxsinx=4xcosx²+sin2x
(sinx)´=cosx, (cosx)´=-sinx, 2sinxcosx=sin2x,c´=0, (f(g(x))´=f´(g(x) . g´(x)
(sinx², f=sint, t=x², (sinx²)´=cost. (x²)´=cosx². 2x=2xcosx²)
f´(x)=2cosx² . 2x -2cosx.(-sinx)=4xcosx²+2cosxsinx=4xcosx²+sin2x
(sinx)´=cosx, (cosx)´=-sinx, 2sinxcosx=sin2x,c´=0, (f(g(x))´=f´(g(x) . g´(x)
(sinx², f=sint, t=x², (sinx²)´=cost. (x²)´=cosx². 2x=2xcosx²)
Автор ответа:
0
Попытаюсь понять решение, большое вам спасибо!
Автор ответа:
0
Дифференцирование сложной функции

Похожие вопросы
Предмет: Алгебра,
автор: anna653460
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: scacuncarolina
Предмет: Математика,
автор: ylisovskaya1