Предмет: Математика,
автор: Klaussalvatore
Пожалуйста помогите, математика,даю 15 баллов
Приложения:
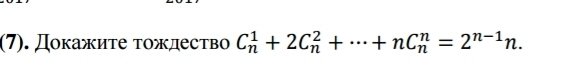
Ответы
Автор ответа:
0
Рассмотрим два случая: n - нечетное и четное.
1) n - нечетное
2) n - четное
При доказательстве тождества применялись формулы:
Бином Ньютона
при a=b=1
Похожие вопросы
Предмет: Английский язык,
автор: keuuahik
Предмет: Русский язык,
автор: kovalevskalana18
Предмет: Математика,
автор: zhusupov339
Предмет: Математика,
автор: миррочка1
Предмет: Математика,
автор: Den26rus1