Предмет: Математика,
автор: bvasek
Помогите сделать задания по высшей математике. Заранее спасибо.
Приложения:
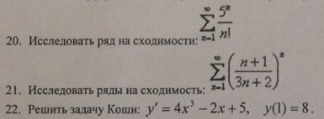
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Биология,
автор: ggpvpp44
Предмет: Қазақ тiлi,
автор: vdydunwsnxicnenskx01
Предмет: Беларуская мова,
автор: veramit228
Предмет: Математика,
автор: КлЭвЭр
Предмет: Математика,
автор: ekazauschkina