Предмет: Алгебра,
автор: QueenOfTheUnion
Найдите все значения x, при которых числовые значения выражений в указанном порядке являются последовательными членами арифметической прогрессии.
Приложения:
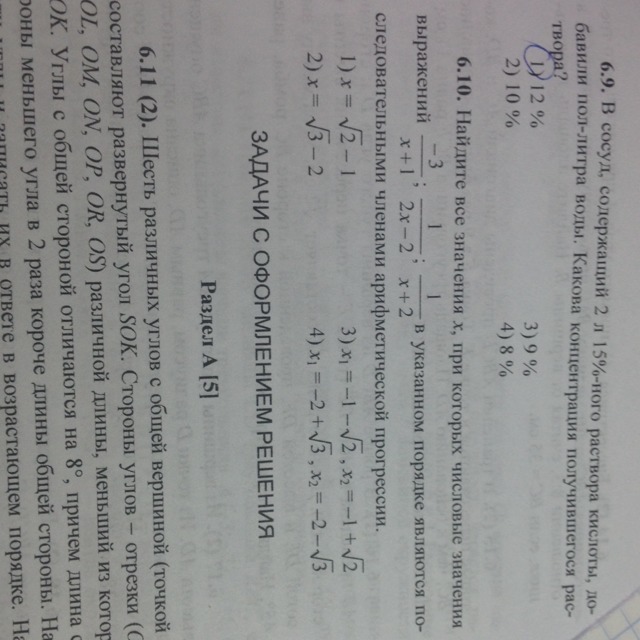
Ответы
Автор ответа:
0
Раз члены прогрессии составляем уравнение:
1/(2x-2)-(-3/x+1)=1/(x+2)-1/(2 x-2) решаем, получаем в числителе
х+1+6(х-1)=2(х-1)-х-1 ⇒ х=1/3
1/(2x-2)-(-3/x+1)=1/(x+2)-1/(2 x-2) решаем, получаем в числителе
х+1+6(х-1)=2(х-1)-х-1 ⇒ х=1/3
Автор ответа:
0
Уравнение составлено верно, но не решено. Ответ неверен.
Автор ответа:
0
Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому соседних членов, т.е.
Уравнение
При х≠ 1; х≠ -2; х ≠ -1
2х²+2х+4х+4 = -6х²+6х-12х+12+2х²-2
6х²+12х-6=0
х²+2х-1=0
D = b² - 4ac
D = 2²- 4*(-1)=4+4=8
√D = √8 = 2√2
x₁ = (-2-2√2)/2= -1 - √2
x₂ = (-2+2√2)/2= -1+√2
Ответ под цифрой 3) x₁ = -1 - √2; x₂ = -1+√2
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Биология,
автор: no45525
Предмет: Геометрия,
автор: physics597
Предмет: Химия,
автор: witalik123
Предмет: Математика,
автор: дашарр