Предмет: Алгебра,
автор: Аноним
Пожалуйста упростите.
Приложения:
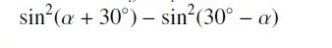
Ответы
Автор ответа:
0
Автор ответа:
0
Гораздо проще выглядит решение, если сначала разложить разность квадратов синусов, а потом применить формулы суммы и разности синусов.
Похожие вопросы
Предмет: Русский язык,
автор: uefasibiri
Предмет: Геометрия,
автор: tttart74
Предмет: Математика,
автор: shamilmamedov48
Предмет: Математика,
автор: belousl
Предмет: Математика,
автор: Знайкавсемирная