Предмет: Математика,
автор: Finndaly2
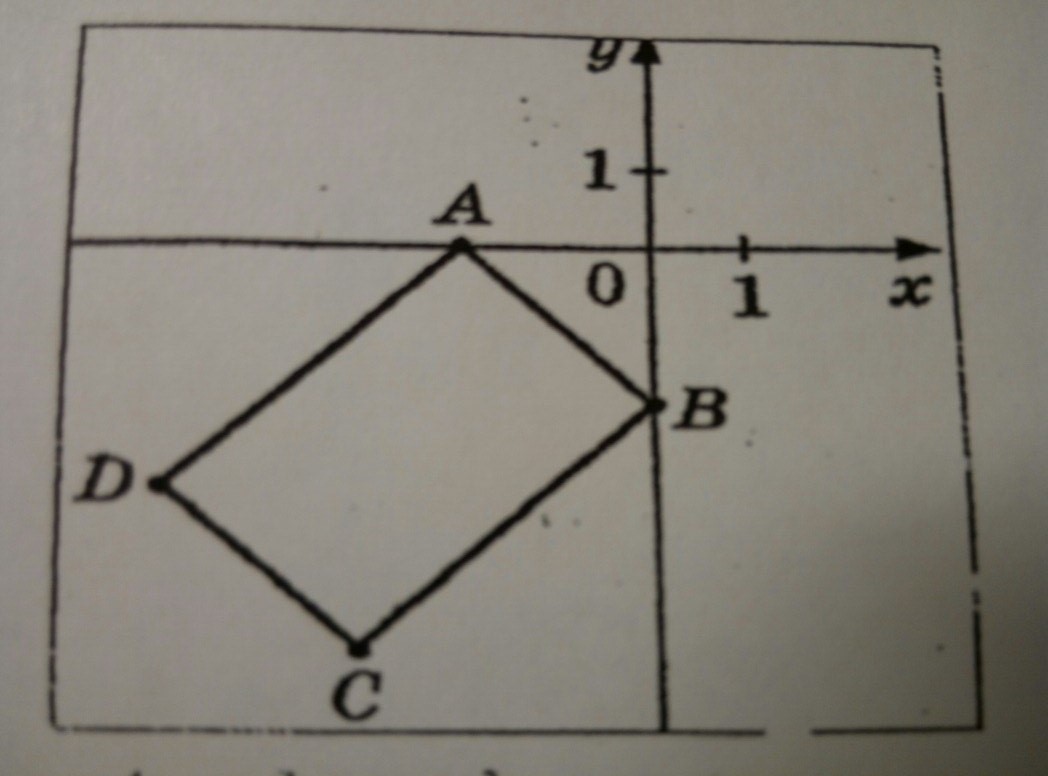
Найдите площадь прямоугольника ,вершины которого заданы координатами в декартовой системе координат A(-2;0),B(0:-2),C(-3,-5),D(-5;-3)
Приложения:
Ответы
Автор ответа:
0
Расм. треугольник АОВ. Катеты ОА=2, ОВ=2. По теореме Пифагора АВ=2√2. Одна сторона найдена. Или можно найти по формуле длины отрезка. Именно по этой формуле удобно найти, например АD=√3²+3²=3√2
теперь можем найти площадь прямоугольника S=2√2·3√2=12
теперь можем найти площадь прямоугольника S=2√2·3√2=12
Автор ответа:
0
Площадь прямоугольника равна произведению длины на ширину
S=AB ·ВС
Найдем длину отрезка АВ =√(0-(-2))²+(-2-0)²=√4+4=√8=2√2
Длина отрезка ВС = √(-3-0))²+(-5-(-2))²=√9+9=√18=3√2
S=2√2·3√2=12 (ед)²
S=AB ·ВС
Найдем длину отрезка АВ =√(0-(-2))²+(-2-0)²=√4+4=√8=2√2
Длина отрезка ВС = √(-3-0))²+(-5-(-2))²=√9+9=√18=3√2
S=2√2·3√2=12 (ед)²
Похожие вопросы
Предмет: Қазақ тiлi,
автор: litvinovdsnil290307
Предмет: Математика,
автор: savscmailru
Предмет: История,
автор: bts781adiyakim
Предмет: Математика,
автор: masha162
Предмет: Алгебра,
автор: sanik3475