Предмет: Математика,
автор: MaRikA97
Помогите пожалуйста....найти интеграл от иррациональной функции
Приложения:
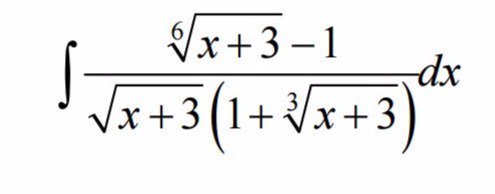
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Окружающий мир,
автор: energoexpertru
Предмет: Физика,
автор: lizas1559
Предмет: Математика,
автор: akhmadovaakhmadova
Предмет: Математика,
автор: ДвоечникЕстПельмени
Предмет: Алгебра,
автор: СнежнаяСова