Предмет: Алгебра,
автор: sasha78789877
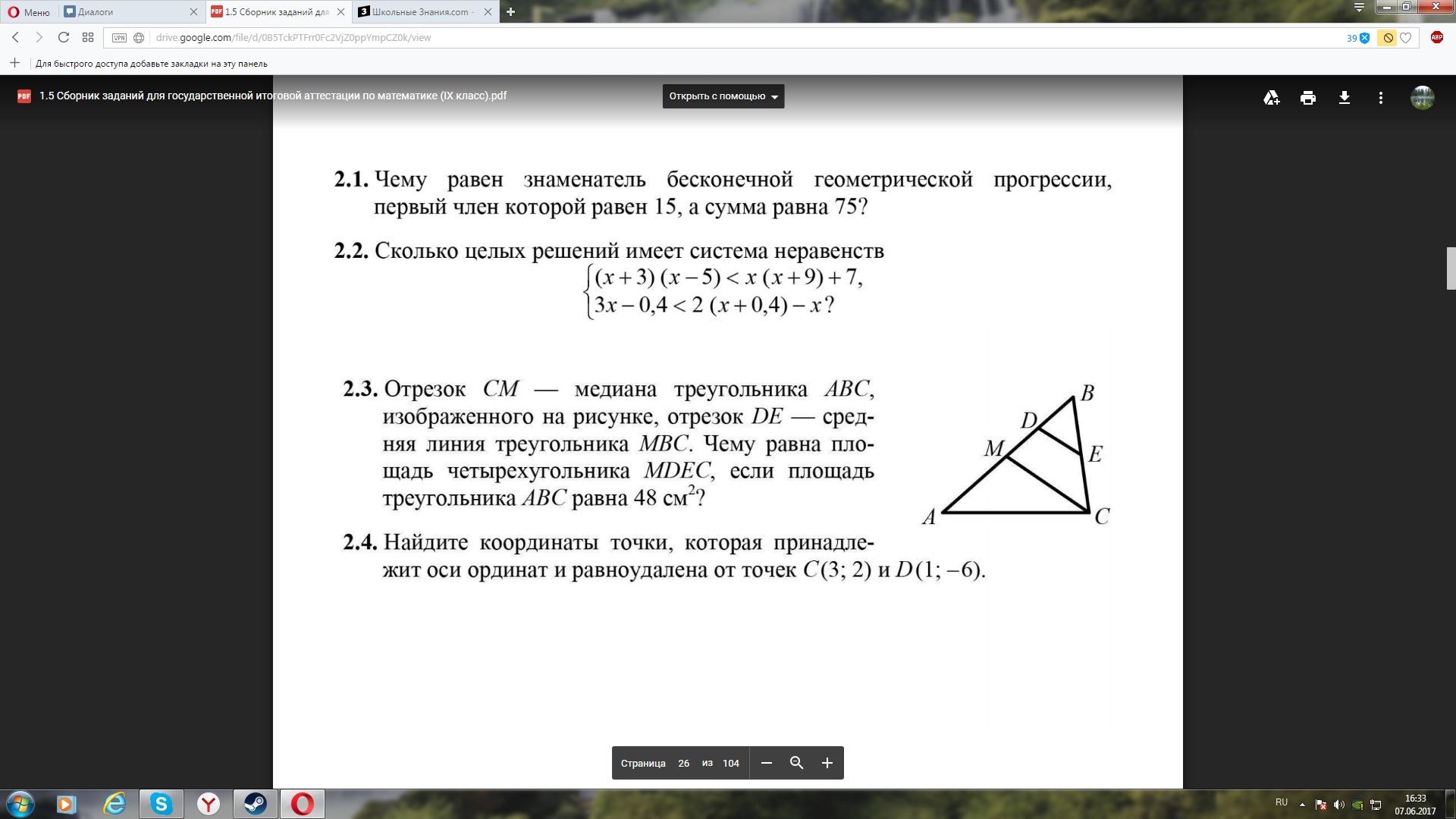
Отрезок СМ - медиана треугольника АВС, изображена на рисунке DE - cредняя линия треугольника МСВ. Чему равна площадь четыреугольника MDEC есле площадь треугольника АВС равна 48см^2? номер:2.3
Приложения:
Ответы
Автор ответа:
0
По свойству медианы треугольники ABC и MBC равновеликие, значит
Smbc=48/2=24
ΔDBE∞ΔMBC по трем углам.
Средняя линия треугольника равна половине его основания, значит
k=1/2*MC/MC=1/2
По свойству подобных треугольников их площади соотносятся как квадрат коэф. подобия
Sdbe/Smbc=(1/2)^2=1/4
Раз площадь ΔDBE составляет 1/4 от площади ΔMBC, то площадь MDEC равна 3/4 площади ΔMBC
Smdec=3/4*24=18
Ответ: 18см^2
Smbc=48/2=24
ΔDBE∞ΔMBC по трем углам.
Средняя линия треугольника равна половине его основания, значит
k=1/2*MC/MC=1/2
По свойству подобных треугольников их площади соотносятся как квадрат коэф. подобия
Sdbe/Smbc=(1/2)^2=1/4
Раз площадь ΔDBE составляет 1/4 от площади ΔMBC, то площадь MDEC равна 3/4 площади ΔMBC
Smdec=3/4*24=18
Ответ: 18см^2
Похожие вопросы
Предмет: Химия,
автор: 0971485285af
Предмет: Информатика,
автор: blacun
Предмет: Алгебра,
автор: 55alisalove55
Предмет: Математика,
автор: 123680