Предмет: Геометрия,
автор: Юлия58
Одна из диагоналей ромба на 4 см больше другой, а площадь равна 96 см квадратных.Найти стороны ромба.
Ответы
Автор ответа:
0
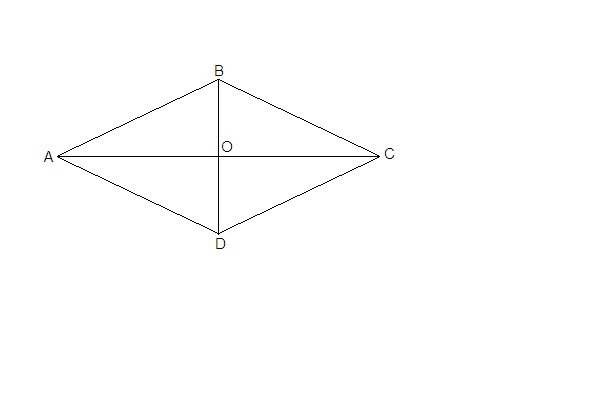
Пусть BD = x, AC = x + 4
Sabcd = (AC·BD)/2
x(x + 4)/2 = 96
x² + 4x - 192 = 0
D/4 = 4 + 192 = 196
x = - 2 + 14 = 12 x = - 2 - 14 = -16 не подходит по смыслу задачи
BD = 12 см, АС = 16 см
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.
ΔАОВ: ∠АОВ = 90°, АО = АС/2 = 8 см, ВО = BD/2 = 6 см
по теореме Пифагора
АВ = √(АО² + ВО² ) = √(64 + 36) = 10 см
У ромба все стороны равны.
Ответ: 10 см.
Sabcd = (AC·BD)/2
x(x + 4)/2 = 96
x² + 4x - 192 = 0
D/4 = 4 + 192 = 196
x = - 2 + 14 = 12 x = - 2 - 14 = -16 не подходит по смыслу задачи
BD = 12 см, АС = 16 см
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам.
ΔАОВ: ∠АОВ = 90°, АО = АС/2 = 8 см, ВО = BD/2 = 6 см
по теореме Пифагора
АВ = √(АО² + ВО² ) = √(64 + 36) = 10 см
У ромба все стороны равны.
Ответ: 10 см.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: zzukova19
Предмет: Математика,
автор: kimaleksandra2901
Предмет: История,
автор: fruk34
Предмет: Алгебра,
автор: настюханаама
Предмет: Геометрия,
автор: еееее