Предмет: Математика,
автор: dudenkoya
Радиус окружности, описанной около треугольника, равна 11 корней из 3. Найдите сторону треугольника
Ответы
Автор ответа:
0
Условие неполное. Добавлю в условии, что треугольник правильный.
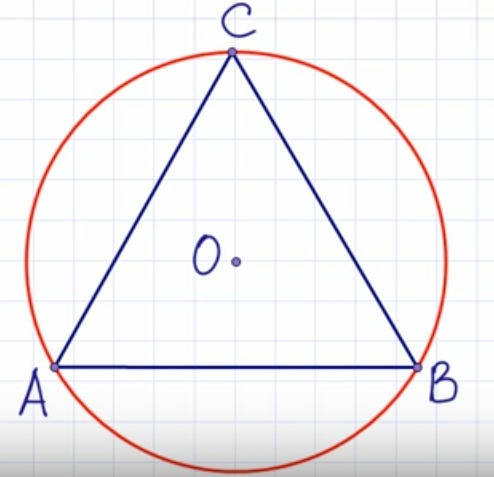
Задача. Радиус окружности, описанной около правильного треугольника, равна 11 корней из 3. Найдите сторону треугольника.
Решение:
Можно найти сторону треугольника через готовые формулы, но покажу как это можно доказать формулу
Обозначим стороны треугольника AC = BC = AB = a(стороны у прав. треугольника равны ведь).
Применим обобщенную теорему синусов:
У правильного треугольника все углы по 60°, следовательно
Получим:
Ответ: 33.
Приложения:
Похожие вопросы
Предмет: География,
автор: nikolchen21
Предмет: Химия,
автор: ggghfyhjjnnzxt44
Предмет: Английский язык,
автор: motosashka
Предмет: Математика,
автор: 77777нннн
Предмет: Химия,
автор: КатюнькаНа