Предмет: Алгебра,
автор: Globadmin
Найти производные dz/dx и dz/dy функции z=z(u,v), где u=u(x;y) и v=(x;y)
Приложения:
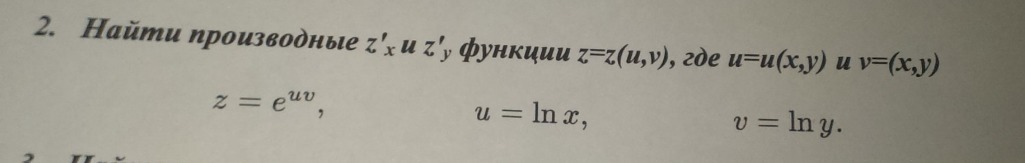
Ответы
Автор ответа:
0
dz/du = v*e^(uv); dz/dv = u*e^(uv)
du/dx = 1/x; du/dy = 0 (потому что y в функции u вообще нет)
dv/dx = 0; dv/dy = 1/y.
dz/dx = dz/du*du/dx + dz/dv*dv/dx = v*e^(uv)*1/x + u*e^(uv)*0 = v/x*e^(uv)
dz/dy = dz/du*du/dy + dz/dv*dv/dy = v*e^(uv)*0 + u*e^(uv)*1/y = u/y*e^(uv)
du/dx = 1/x; du/dy = 0 (потому что y в функции u вообще нет)
dv/dx = 0; dv/dy = 1/y.
dz/dx = dz/du*du/dx + dz/dv*dv/dx = v*e^(uv)*1/x + u*e^(uv)*0 = v/x*e^(uv)
dz/dy = dz/du*du/dy + dz/dv*dv/dy = v*e^(uv)*0 + u*e^(uv)*1/y = u/y*e^(uv)
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: gyggyyyg9
Предмет: Русский язык,
автор: pinklady18
Предмет: Математика,
автор: денисмуравлев142
Предмет: История,
автор: afina111