Question

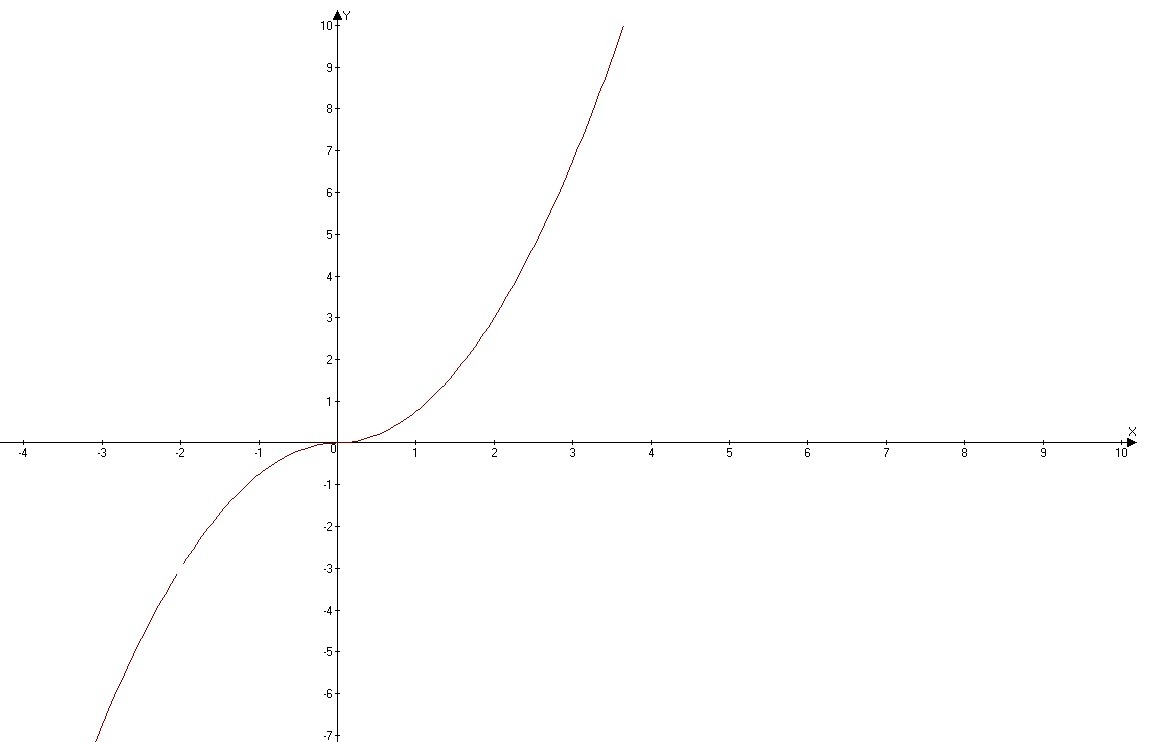
Постройте график функции.

Определите, при каких значениях m прямая y=m не имеет с графиком ни одной о$y= frac{(0,75 x^{2} +1,5x)|x| }{x+2}$бщей точки.

Answer 1

$displaystyle y= dfrac{(0.75x^2+1.5x)|x|}{x+2} = dfrac{0.75x(x+2)|x|}{x+2}= 0.75x|x|=\ \ \ = left { {{0.75x^2,,,,, if,,,,, x geq 0} atop {-0.75x^2,,,,, if,,,,, x leq 0}} right.$

Графиком функции является парабола(первый график ветви которого направлены вверх, а второй - вниз.)

Область определения данной функции $D(y)=(-infty;-2)cup(-2;+infty)$

$y=m$ - прямая, параллельная оси Ох.

В точке разрыва х=-2 значение функции равно $-0,75cdot (-2)^2=-3$

При $m=-3$ графики не будут пересекаться 

Answer 2

Объясните пж. Почему область такая область определения?

Answer 3

x+2 не равен 0

Answer 4

х не равен -2

Answer 5

Значит область определения это все допустимые значения х, кроме х=-2

Answer 6

Спасибо большое