Предмет: Геометрия,
автор: KettyHiv
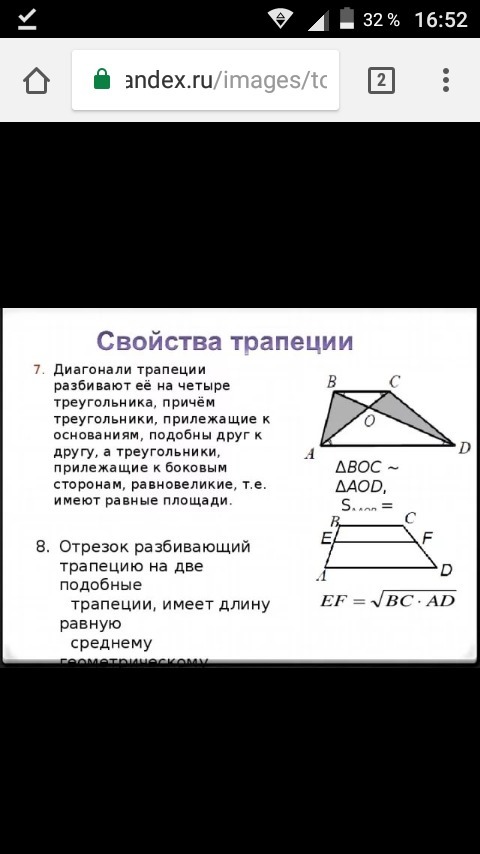
Докажите, что диагонали трапеции делят ее на четыре треугольника, два из которых имеют равные площади, а площади двух других относятся как квадраты оснований.
Ответы
Автор ответа:
0
построим трапеци. ABCD.проведём диагонали, пересекающиеся в точке O.
рассмотрим треугольники ABD и ACD.они равны, так как имеют общее основание AD и одинаковые высоты. (если провести их из точек B и C.тогда S(ABO) + S(AOD) = S(COD) + S (AOD) => S(ABO) = S(COD).
рассмотрим треугольники ABD и ACD.они равны, так как имеют общее основание AD и одинаковые высоты. (если провести их из точек B и C.тогда S(ABO) + S(AOD) = S(COD) + S (AOD) => S(ABO) = S(COD).
Приложения:
Автор ответа:
0
Хорошо, а что насчет второй части доказательства, где площади двух других треугольников относятся как квадраты основания?
Похожие вопросы
Предмет: Математика,
автор: vladPunn
Предмет: Русский язык,
автор: Аноним
Предмет: Литература,
автор: okomary
Предмет: Математика,
автор: pobeda2003mih