Предмет: Алгебра,
автор: Maryn8
Как решить этот пример?
Приложения:
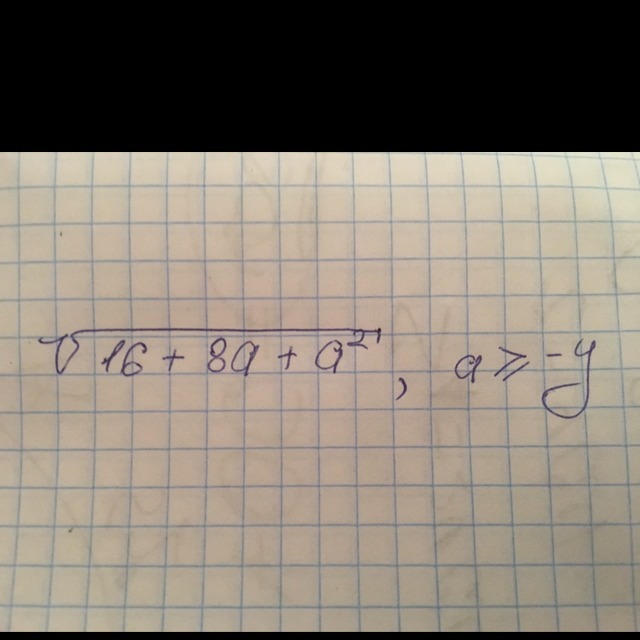
Ответы
Автор ответа:
0
Т.к. а^2+8а+16=(а+4)^2, то данное на фото иррациональное выражение выносится под модулем, отсюда следует, что |а+4| является корнем (а+4)^2 . Если а = -у, получается либо -(-у+4) либо (-у+4):
-(-у+4)=у-4 ,а (-у+4)=4-у
Но все же это не является ответом, т.к. значение модуля, указанного выше может быть равно нулю.
Поэтому предположим, что -(-у+4)=(-у+4)=0
Значит 4-у=0 и у-4=0
Итак в обоих случаях при значении модуля равном нулю у=4, то получается а = -4 = -у
Но не забудем, что а также может быть больше -у. Значет ответ записываем ввиде
числового промежутка а=[-4;+бесконечность] (если значение модуля равно 0) Но я также могу рассмотреть данное выражение при положительном либо отрицательном значении модуля. Если хотите.
-(-у+4)=у-4 ,а (-у+4)=4-у
Но все же это не является ответом, т.к. значение модуля, указанного выше может быть равно нулю.
Поэтому предположим, что -(-у+4)=(-у+4)=0
Значит 4-у=0 и у-4=0
Итак в обоих случаях при значении модуля равном нулю у=4, то получается а = -4 = -у
Но не забудем, что а также может быть больше -у. Значет ответ записываем ввиде
числового промежутка а=[-4;+бесконечность] (если значение модуля равно 0) Но я также могу рассмотреть данное выражение при положительном либо отрицательном значении модуля. Если хотите.
Похожие вопросы
Предмет: Русский язык,
автор: zhalgasaiyim
Предмет: Математика,
автор: kylunuchroman2612
Предмет: Астрономия,
автор: vasilisaganenkova
Предмет: Математика,
автор: isaego23
Предмет: Математика,
автор: Аноним