Предмет: Алгебра,
автор: NikitaP4ck
а) Решите уравнение:
4*16^sinx-9*4^sinx+2=0
б) Выберите корни на отрезке [5pi/2; 4pi]
Ответы
Автор ответа:
0
Решение на фотографии. Отбирал двумя способами. Но по окружности легче:))) Первый корень тоже можно отобрать по окружности, это к 5п/2+п=7п/2
Приложения:

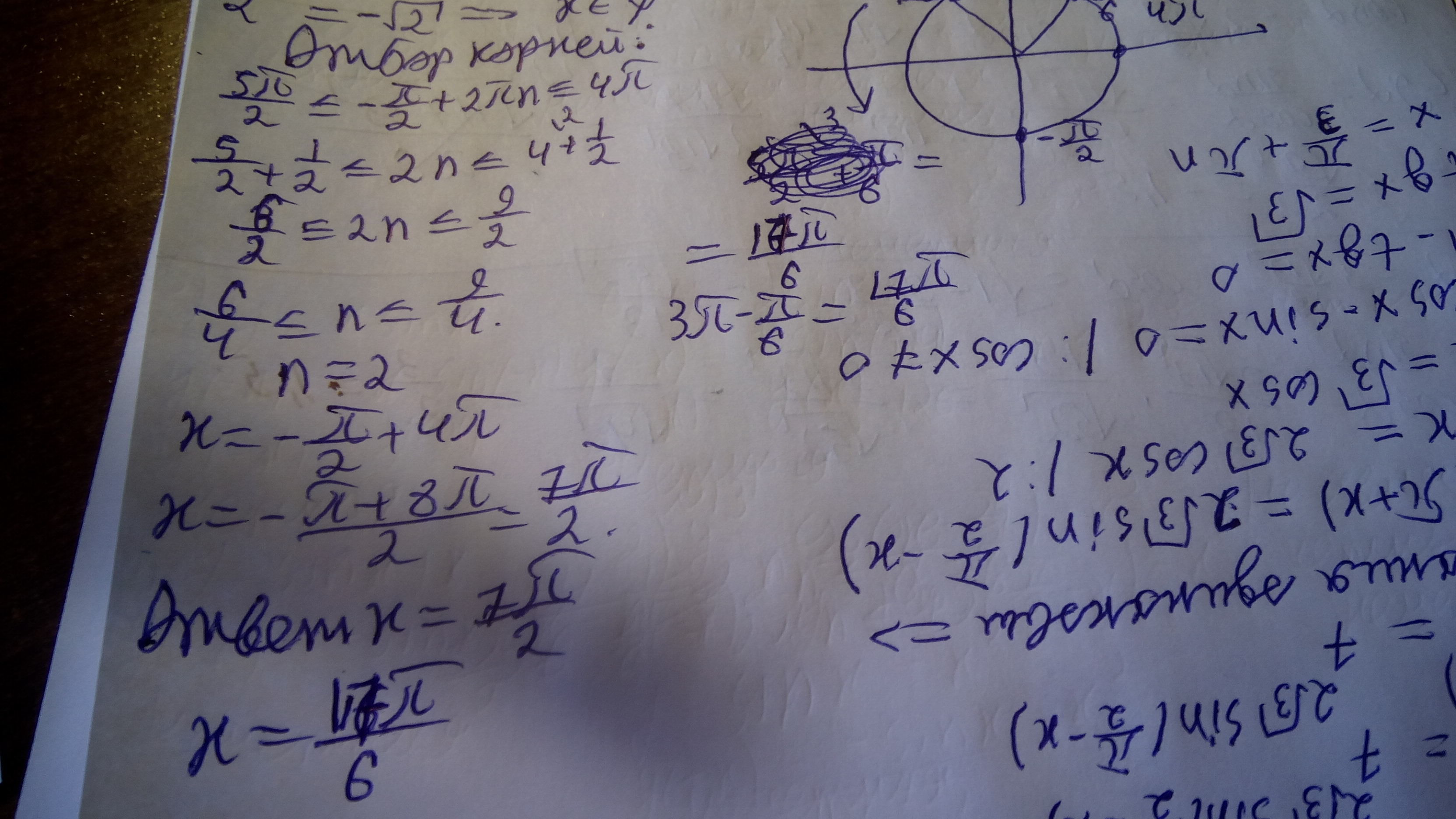
Автор ответа:
0
Приложения:

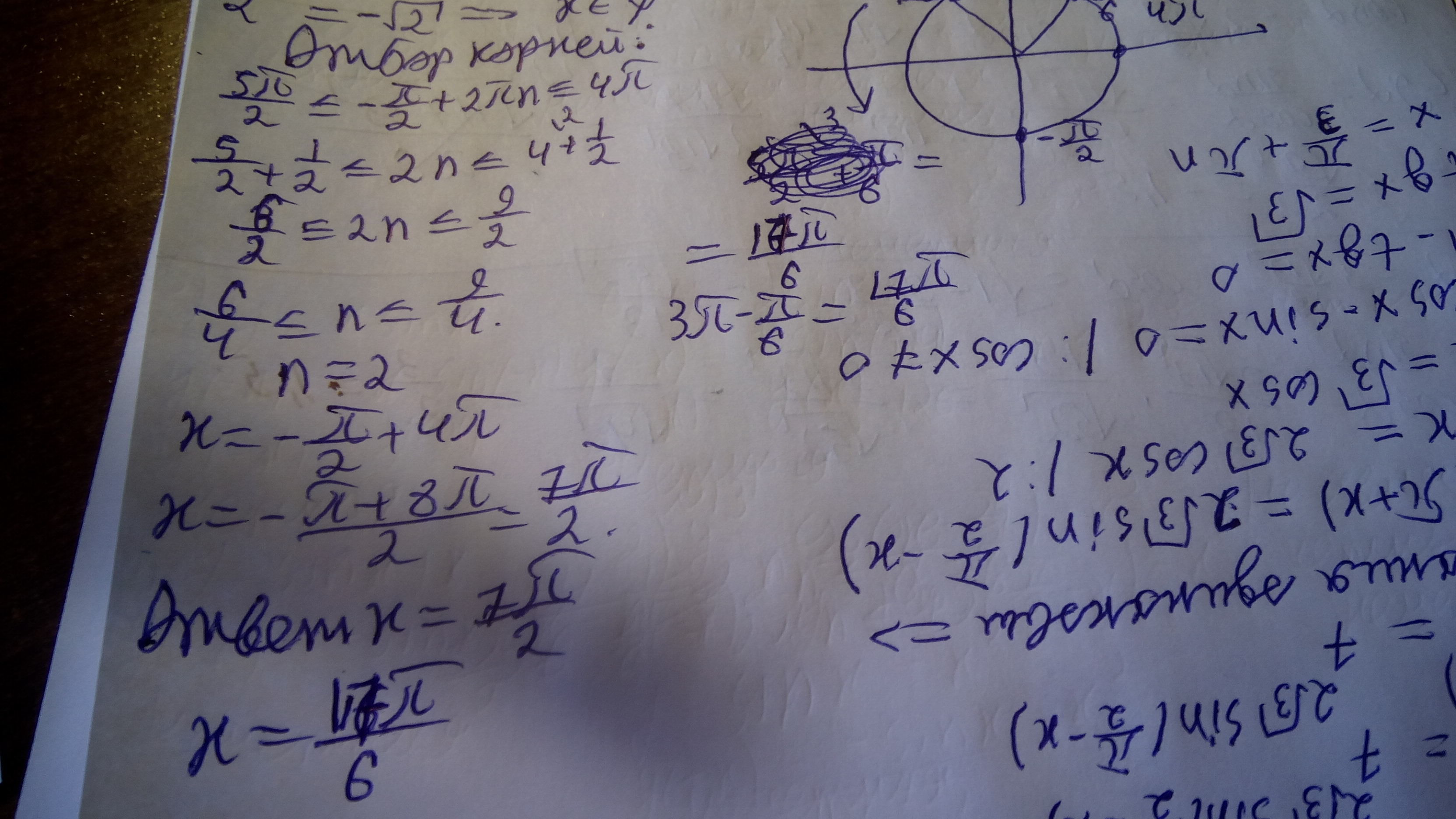
Похожие вопросы
Предмет: Алгебра,
автор: lozuakmaria15
Предмет: Английский язык,
автор: snowleo1405
Предмет: Математика,
автор: ohremenkoivan2505
Предмет: Информатика,
автор: Аноним
Предмет: Математика,
автор: Аноним