Предмет: Математика,
автор: leopold1998g
Найдите значение выражения
sqrt(2)-2*sqrt(2)*sin^2(15pi/8)
Приложения:
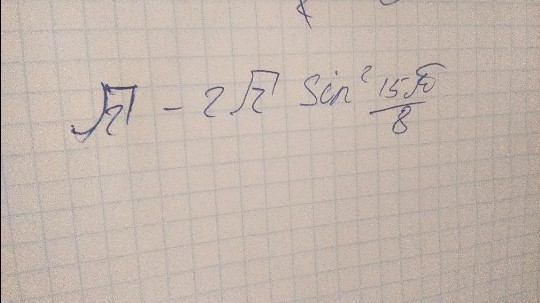
Ответы
Автор ответа:
0
P.S.
Автор ответа:
0
=√2*(1-2*sin² 15π/8)=√2*cos(2*15π/8)=√2*cos(15π/4)=
=√2*cos(4π-π/4)=√2*cos(π/4)=√2*√2/2=2/2=1
=√2*cos(4π-π/4)=√2*cos(π/4)=√2*√2/2=2/2=1
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Биология,
автор: beka20090905
Предмет: Қазақ тiлi,
автор: orazbaevakausar0
Предмет: Физика,
автор: 2003margo
Предмет: Математика,
автор: marlen373