Предмет: Геометрия,
автор: westgeirgraf
Окружности с центрами в точках P и O пересекаются в точках A и B, причём точки P и O лежат по разные стороны от прямой AB. Докажите, что AB перпендикулярно PO.
Ребят.....
Ответы
Автор ответа:
0
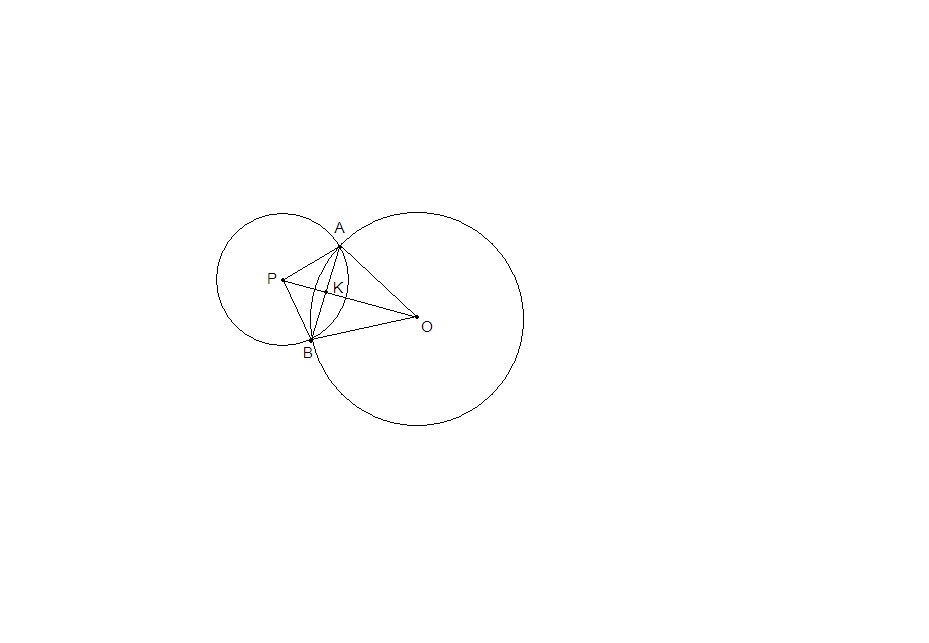
Надо центры окружностей соединить с точками А и В.
Пусть К - середина АВ.
РА = РВ как радиусы, ⇒ ΔРАВ равнобедренный, ⇒ РК - медиана и высота, т.е. РК⊥АВ
ОА = ОВ как радиусы, ⇒ ΔОАВ равнобедренный, ⇒ ОК - медиана и высота, т.е. ОК⊥АВ.
Через одну точку К можно провести единственную прямую, перпендикулярную АВ, ⇒ РК и ОК лежат на одной прямой.
Значит, РО⊥АВ.
Пусть К - середина АВ.
РА = РВ как радиусы, ⇒ ΔРАВ равнобедренный, ⇒ РК - медиана и высота, т.е. РК⊥АВ
ОА = ОВ как радиусы, ⇒ ΔОАВ равнобедренный, ⇒ ОК - медиана и высота, т.е. ОК⊥АВ.
Через одну точку К можно провести единственную прямую, перпендикулярную АВ, ⇒ РК и ОК лежат на одной прямой.
Значит, РО⊥АВ.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: abdinasyriska5
Предмет: Алгебра,
автор: ffctfcgygcyg
Предмет: Қазақ тiлi,
автор: shaperinaevelina2004
Предмет: Математика,
автор: gasanovisa1