Предмет: Алгебра,
автор: alexxx20000
Помогите решить два примера Срочно надо
32*2^√x-1=4^√x-1
Приложения:
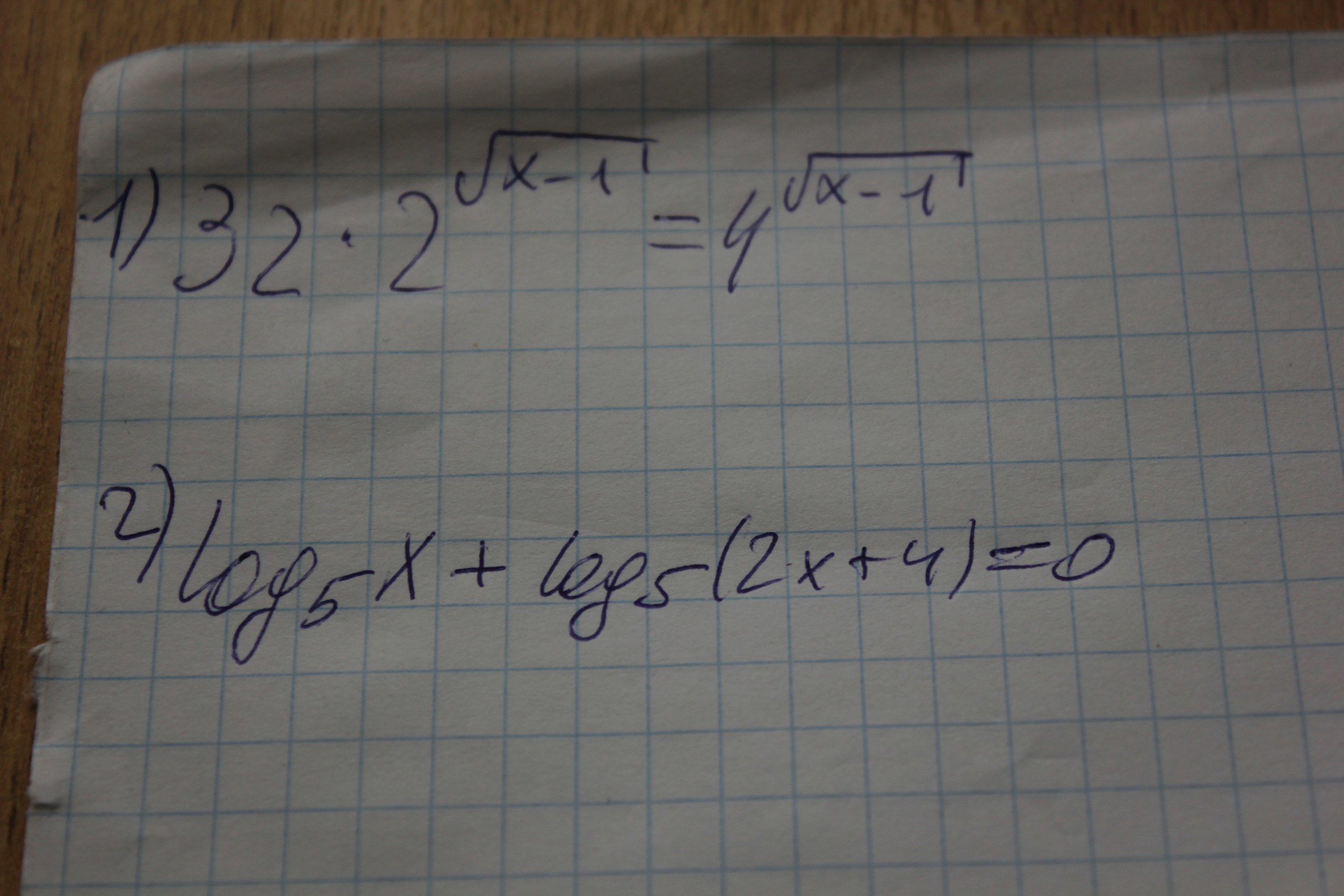
Ответы
Автор ответа:
0
1) Разделив обе части уравнения на 2^(√(x-1)), получим уравнение 32=2^(√(x-1)), или 2⁵=2^(√(x-1)). Отсюда √(x-1)=5, x-1=5²=25, x=25+1=26. Ответ: х=26.
2) Применяя формулу суммы логарифмов, получаем log_5(x*(2*x+4))=0, x*(2*x+4)=5⁰=1, 2*x² +4*x-1=0, дискриминант D=16+8=24=(2*√6)², x1=(-4+2*√6)/4=√6/2-1, x2=(-4-2*√6)/4=-1-2√6. Но так как по свойству логарифма x>0, то x=√6/2-1. Ответ: x=√6/2-1.
2) Применяя формулу суммы логарифмов, получаем log_5(x*(2*x+4))=0, x*(2*x+4)=5⁰=1, 2*x² +4*x-1=0, дискриминант D=16+8=24=(2*√6)², x1=(-4+2*√6)/4=√6/2-1, x2=(-4-2*√6)/4=-1-2√6. Но так как по свойству логарифма x>0, то x=√6/2-1. Ответ: x=√6/2-1.
Автор ответа:
0
Решение смотри на фото
Приложения:

Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: stasmitrofanov21
Предмет: Другие предметы,
автор: Nechanna84
Предмет: История,
автор: Sonia258