Предмет: Геометрия,
автор: zayackitaec02
точка М внутренняя для треугольников АВС. Докажите, что АМ+МС<АВ+ВС. С объяснением.
Ответы
Автор ответа:
0
поторопилась в первый раз))
понятно, что нужно использовать неравенство треугольника...
только нужно найти удобные треугольники...
и неравенства можно складывать))
понятно, что нужно использовать неравенство треугольника...
только нужно найти удобные треугольники...
и неравенства можно складывать))
Приложения:
Автор ответа:
0
спасибо
Автор ответа:
0
task/24810632
---.---.---.---. ---
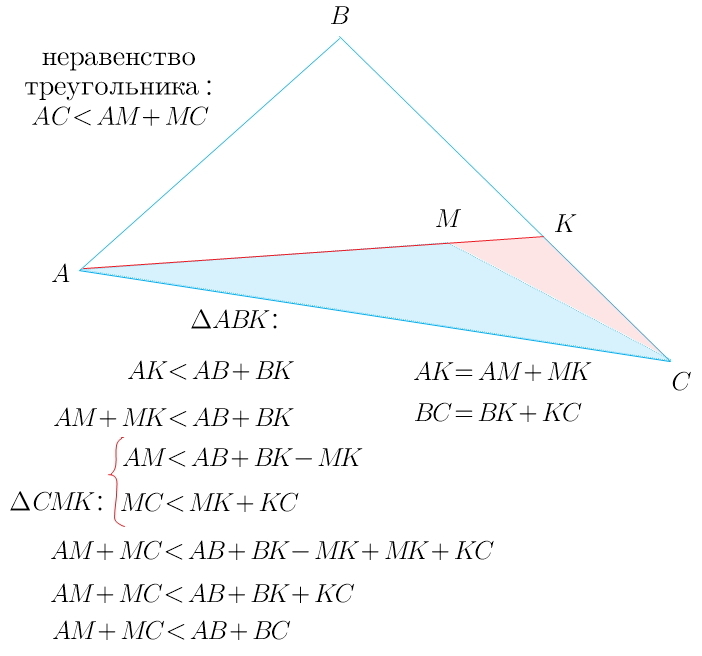
Точка M лежит внутри треугольника ABC.
Докажите, что MA + МС< ВA + BC.
-------------------
Продолжаем отрезок AM до пересечения со стороной BC в точке K
Используем неравенство треугольника
AM +MK < BK+BA (1) * * * для ΔABK * * *
MC < MK +KC (2) * * * для ΔMKC * * *
складывая неравенства (1) и (2) получим :
AM +MK +MC < BK +BA+MK +KC ; * * * BK +KC = BC * * *
MA + MC < BA + BC
см приложение
---.---.---.---. ---
Точка M лежит внутри треугольника ABC.
Докажите, что MA + МС< ВA + BC.
-------------------
Продолжаем отрезок AM до пересечения со стороной BC в точке K
Используем неравенство треугольника
AM +MK < BK+BA (1) * * * для ΔABK * * *
MC < MK +KC (2) * * * для ΔMKC * * *
складывая неравенства (1) и (2) получим :
AM +MK +MC < BK +BA+MK +KC ; * * * BK +KC = BC * * *
MA + MC < BA + BC
см приложение
Приложения:

Похожие вопросы
Предмет: Українська мова,
автор: liubovkonstantinova
Предмет: История,
автор: gatery666
Предмет: Математика,
автор: alen4ik199420
Предмет: Математика,
автор: Hanjaa