Question

вычислите площадь фигуры ограниченной линиями y=x^2-5x+6 и y=0 помогите пжл

Answer 1

Ответ:

S=1/6 (кв. единица)

Пошаговое объяснение:

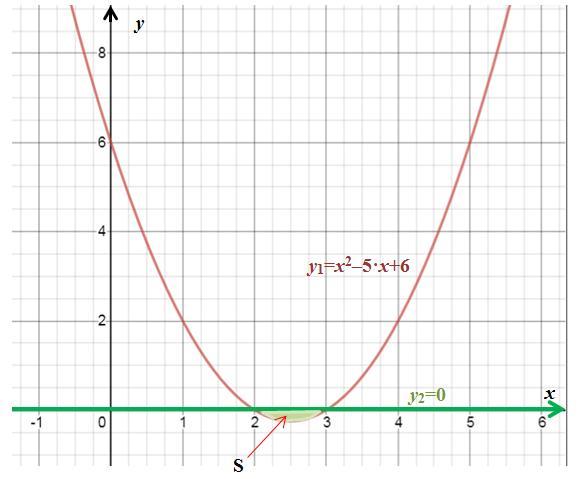
Сначала определим точки пересечений функции y₁= x²–5•x+6 и y₂=0 (то есть, ось абсцисс; см. рисунок). Для этого приравниваем функции:

y₁=y₂ ⇔ x²–5•x+6=0 ⇔ (x–2)•(x–3)=0 ⇔ x₁=2, x₂=3.

Площадь S фигуры вычислим с помощью определенного интеграла:

$\displaystyle S=\int\limits^3_{2} {(y_{2}-y_{1} )} \, dx =\int\limits^3_{2} {(0-(x^{2}-5\cdot x+6))} \, dx =\int\limits^3_{2} {(-x^{2}+5\cdot x-6)} \, dx \\\\=(-\frac{x^{3} }{3} +\frac{5 \cdot x^{2} }{2} -6\cdot x) \left \ / {{3} \atop {2}} \right. =(-\frac{3^{3} }{3} +\frac{5 \cdot 3^{2} }{2} -6\cdot 3 )-(-\frac{2^{3} }{3} +\frac{5 \cdot 2^{2} }{2} -6\cdot 2 )=\\\\=(-9+22\frac{1}{2}-18)-(-2\frac{2}{3}+10-12)=-4\frac{1}{2}+4\frac{2}{3}=\frac{1}{6}.$