Предмет: Геометрия,
автор: LюблЮМузыкУ
Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135 градусам.
Ответы
Автор ответа:
33
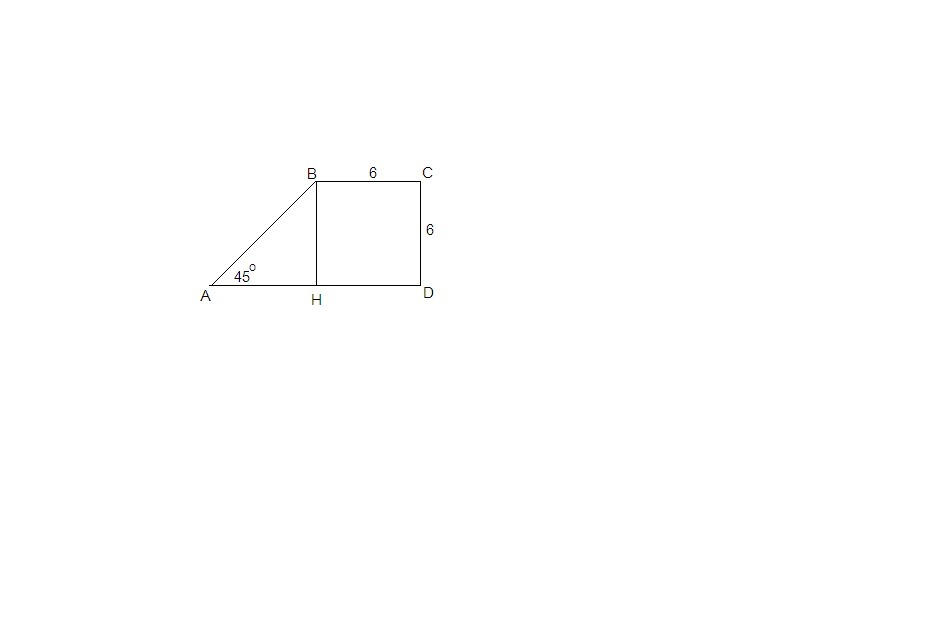
В прямоугольной трапеции ABCD меньшие стороны BC = CD = 6 см, больший угол АВС = 135°.
Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, значит, угол ВАD = 45°.
Проведем высоту ВН.
BCDH - квадрат, т.к. BC║HD (основания трапеции), ВН ║ CD как два перпендикуляра к одной прямой, углы по 90° и ВС = CD. ⇒
ВН = CD = 6 см.
В ΔАВН: ∠H = 90°, ∠A = 45° ⇒ ∠B = 45° ⇒ треугольник равнобедренный, AH = BH = 6 см. ⇒ AD = AH + HD = 6 + 6 = 12 см.
S = (AD + BC)/2 · BH = (12 + 6)/2 · 6 = 9 · 6 = 54 (см²)
Сумма углов, прилежащих к боковой стороне трапеции, равна 180°, значит, угол ВАD = 45°.
Проведем высоту ВН.
BCDH - квадрат, т.к. BC║HD (основания трапеции), ВН ║ CD как два перпендикуляра к одной прямой, углы по 90° и ВС = CD. ⇒
ВН = CD = 6 см.
В ΔАВН: ∠H = 90°, ∠A = 45° ⇒ ∠B = 45° ⇒ треугольник равнобедренный, AH = BH = 6 см. ⇒ AD = AH + HD = 6 + 6 = 12 см.
S = (AD + BC)/2 · BH = (12 + 6)/2 · 6 = 9 · 6 = 54 (см²)
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: nazekebak
Предмет: Геометрия,
автор: tailgame228
Предмет: Английский язык,
автор: a00405182
Предмет: Русский язык,
автор: kmurodalieva
Предмет: Геометрия,
автор: JavaramoyaCarica