Предмет: Математика,
автор: PelageaM
Помогите пожалуйста, найдите значения x, при которых значение производной функции f(x) равно 0, если f(x)=1/2x+sin(x-П/3)
Ответы
Автор ответа:
0
f'(x)=1/2+cos(x-Pi/3)
1/2+cos(x-Pi/3) = 0
cos(x-Pi/3) = -1/2
x - Pi/3 = +- arccos(-1/2) + 2Pi*k, k прин Z
x - Pi/3 = +- (Pi - arccos(1/2)) + 2Pi*k, k прин Z
x - Pi/3 = +- (Pi - Pi/3) + 2Pi*k, k прин Z
x - Pi/3 = +- (2Pi/3) + 2Pi*k, k прин Z
x = +- (2Pi/3) + Pi/3 + 2Pi*k, k прин Z
1/2+cos(x-Pi/3) = 0
cos(x-Pi/3) = -1/2
x - Pi/3 = +- arccos(-1/2) + 2Pi*k, k прин Z
x - Pi/3 = +- (Pi - arccos(1/2)) + 2Pi*k, k прин Z
x - Pi/3 = +- (Pi - Pi/3) + 2Pi*k, k прин Z
x - Pi/3 = +- (2Pi/3) + 2Pi*k, k прин Z
x = +- (2Pi/3) + Pi/3 + 2Pi*k, k прин Z
Автор ответа:
0
Держи решение!) Не очень уверена, что правильно, но всё же)
Приложения:
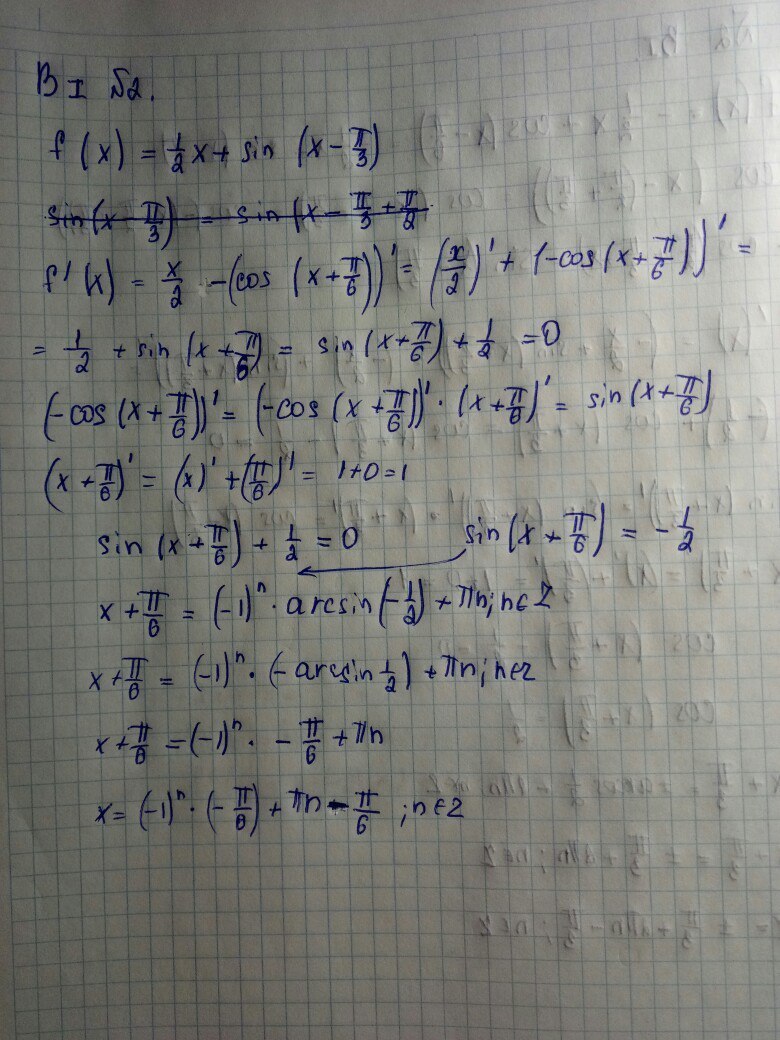
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: MrFunker
Предмет: Математика,
автор: iuliacosonea2002
Предмет: Алгебра,
автор: sitdikova02