Предмет: Алгебра,
автор: pervakoveugeny
y=1/2(|x/2-2/x|+x/2+2/x) постройте график функции
Определите при каких значениях m прямая y=m имеет с графиком ровно одну общую точку
Ответы
Автор ответа:
0
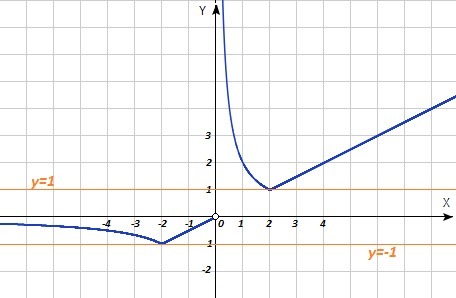
Область определения функции: x≠0; D(y) = (-∞; 0)∪(0; +∞)
Раскрываем модуль
Метод интервалов
---------- [-2] ++++++++ (0) ----------- [2] ++++++++ -> x
x ∈ [-2; 0) ∪ [2; +∞)
y = 0,5 x - линейная функция, график - прямая линия. Точки для построения
x₁ = 2; y₁ = 1; x₂ = -2; y₂ = -1
Метод интервалов
---------- (-2) ++++++++ (0) ----------- (2) ++++++++ -> x
x ∈ (-∞;-2) ∪ (0; 2)
y = 2/x - гипербола. Точки для построения
x₁ = -4; y₁ = -0,5; x₂ = -3; y₂ = -2/3; x₃ = 1/2; y₃ = 4; x₄ = 1; y₄ = 2
Прямая y=m имеет одну точку пересечения при m = 1 и m = -1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ilqar230
Предмет: Физика,
автор: sashakovalchuk020
Предмет: История,
автор: gagaggagagagga
Предмет: История,
автор: max3d2610
Предмет: Информатика,
автор: dimaSB