Предмет: Алгебра,
автор: macs2601
Помогите решить уравнение!
Приложения:
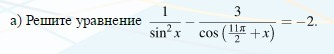
Ответы
Автор ответа:
0
1/sin²x-3/(cos(11π/2+x))=-2 ОДЗ: sinx≠0 x≠πn
1/sin²x-3/(cos(10π+π/2+x))=-2
1/sin²x-3/cos(π/2+x)=-2
1/sin²x-3/(-sinx)=-2
1/sin²x+3/sinx=-2 |×sin²x
1+3*sinx=-2*sin²x
2*sin²x+3*sinx+1=0
sinx=t ⇒
2t²+3t+1=0 D=1
t₁=-1 sinx=-1 x₁=3π/2+2πn
t₂=-0,5=-1/2 sinx=-1/2 x₂=-π/6+2πn x₃=7π/6+2πn.
Ответ: x₁=3π/2+2πn x₂=-π/6+2πn x₃=7π/6+2πn.
1/sin²x-3/(cos(10π+π/2+x))=-2
1/sin²x-3/cos(π/2+x)=-2
1/sin²x-3/(-sinx)=-2
1/sin²x+3/sinx=-2 |×sin²x
1+3*sinx=-2*sin²x
2*sin²x+3*sinx+1=0
sinx=t ⇒
2t²+3t+1=0 D=1
t₁=-1 sinx=-1 x₁=3π/2+2πn
t₂=-0,5=-1/2 sinx=-1/2 x₂=-π/6+2πn x₃=7π/6+2πn.
Ответ: x₁=3π/2+2πn x₂=-π/6+2πn x₃=7π/6+2πn.
Похожие вопросы
Предмет: Английский язык,
автор: zzzvk2015
Предмет: Алгебра,
автор: Аноним
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: nastyushakayuk