Предмет: Математика,
автор: LJJIK
Исследовать на сходимость несобственный интеграл, не вычисляя его.
Приложения:
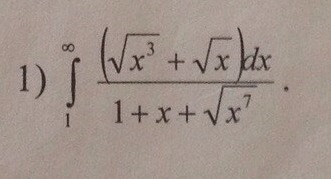
Ответы
Автор ответа:
0
Этот несобственный интеграл сходится по первому признаку сравнения
сходится по первому признаку сравнения
Значит, данный несобственный интеграл сходится
Похожие вопросы
Предмет: Математика,
автор: BSST777
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: FriskTH6868
Предмет: Геометрия,
автор: yusicim
Предмет: Математика,
автор: рыбка1986