Question

ПЛАНИМЕТРИЯ

В равнобедренный треугольник с основанием в 12 см вписана окружность и к ней проведены три касательные так, что они отсекают от данного треугольника три малых треугольника. Сумма периметров малых треугольников равна 48 см. Найти боковую сторону данного треугольника. Выполните, пожалуйста, чертеж.

Спасибо заранее

Answer 1

Дано:
Треугольник АВС, АВ=ВС, АС=12 см
Окружность с центром в точке О вписана в треугольник АВС.
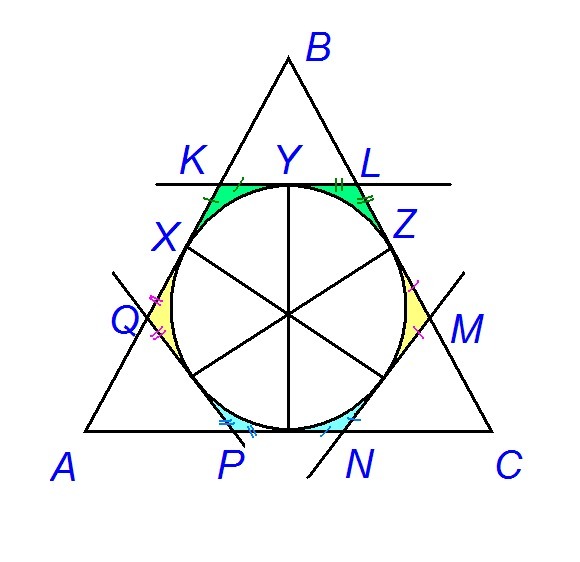
KL, MN, PQ - касательные.
P(KBL) + P(MCN) + P(PAQ) = 48 см

Найти: АВ

Решение:
Проведем радиусы окружности в точки касания (OX, OY, OZ и другие).
Рассмотрим треугольник KBL. Отрезки касательных, проведенные из одной точки, равны. Значит, KX=KY, LY=LZ. Таким образом, периметр треугольника KBL можно переписать в виде:
Р(KBL)=BK+BL+KY+LY=BK+BL+KX+LZ
Аналогично, можно переписать выражения для периметров треугольников MCN и PAQ (очередной отрезок заменяется на равный, который в отличие от предыдущего является частью периметра треугольника АВС).
Получившаяся сумма периметров всех трех треугольников будет равна периметру треугольника АВС.
P(KBL) + P(MCN) + P(PAQ) = P(АВС) = 48
P(АВС) = AB+ BC + AC
Так как треугольник равнобедренный, то:
P(АВС) = 2AB+ AC
Подставляем известные величины:
48 = 2AB+ 12
2AB = 36
АВ = 18 (см)
Ответ: 18 см