Предмет: Математика,
автор: n4rut016
Помогите решить тригометрические уравнения
Приложения:
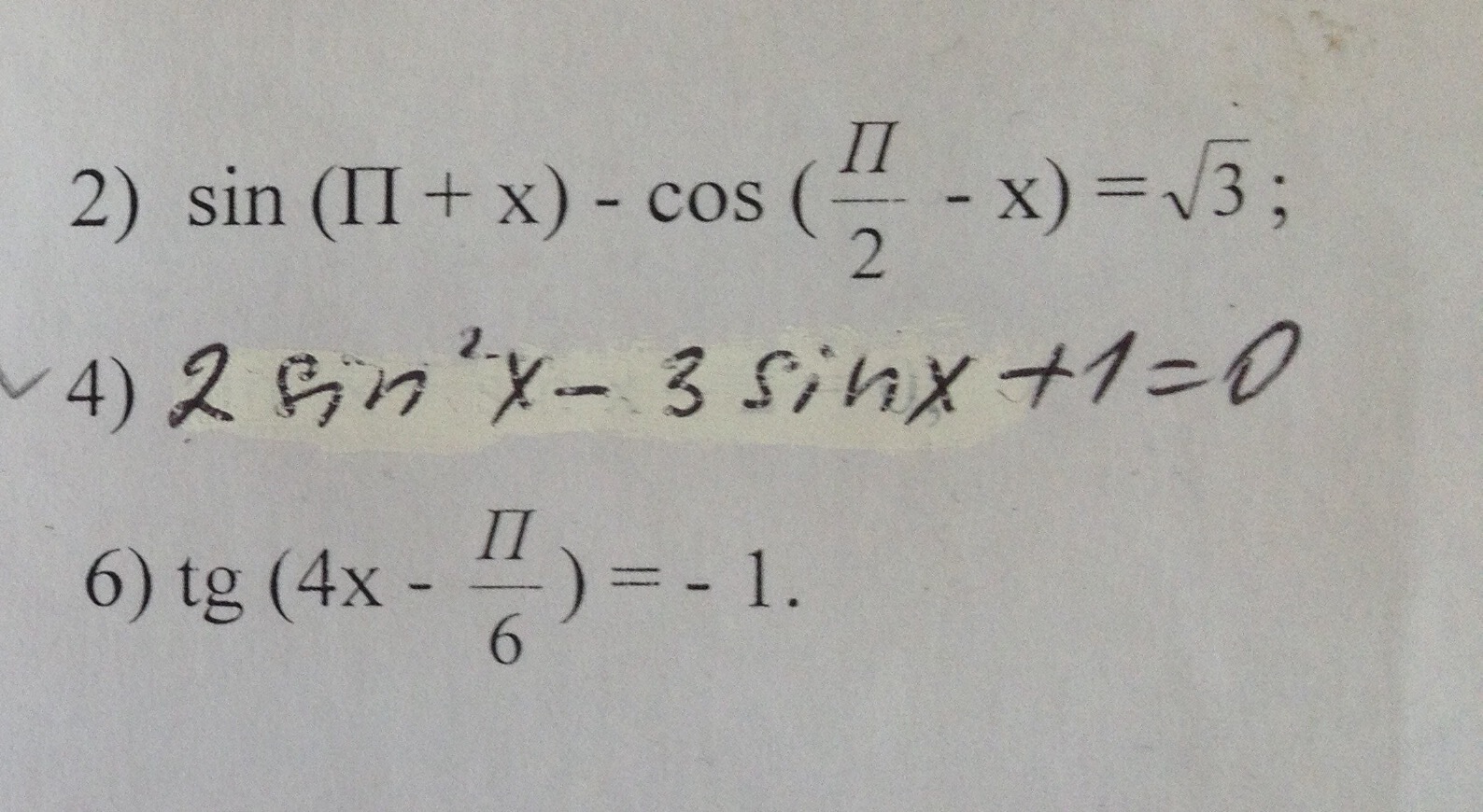
Ответы
Автор ответа:
0
1. sin (Pi + x) - cos (Pi/2 - x) = sqrt(3)
-sinx - sinx = sqrt(3)
-2sinx = sqrt(3)
sinx = -sqrt(3)/2
x = (-1)^k arcsin(-sqrt(3)/2) + Pik, k прин Z
x = (-1)^(k+1) arcsin(sqrt(3)/2) + Pik, k прин Z
x = (-1)^(k+1) Pi/3 + Pik, k прин Z
===================
2. 2sin^2x - 3sinx + 1 = 0
sinx = t, -1 <= t <= 1
2t^2 - 3t + 1 = 0
D = 9 - 4*2*1 = 1
t1 = (3 + 1)/4 = 1
t2 = (3 - 1)/4 = 1/2
sinx = 1
x = (-1)^k arcsin1 + Pik, k прин Z
x = (-1)^k Pi/2 + Pik, k прин Z
sinx = 1/2
x = (-1)^k arcsin(1/2) + Pik, k прин Z
x = (-1)^k Pi/6 + Pik, k прин Z
===================
6. tg(4x - Pi/6) = -1
4x - Pi/6 = arctg(-1) + Pik, k прин Z
4x - Pi/6 = -arctg(1) + Pik, k прин Z
4x - Pi/6 = -Pi/4+ Pik, k прин Z
4x = -Pi/4 + Pi/6 + Pik, k прин Z
4x = -Pi/12 + Pik, k прин Z
x = -Pi/48 + Pik/4, k прин Z
-sinx - sinx = sqrt(3)
-2sinx = sqrt(3)
sinx = -sqrt(3)/2
x = (-1)^k arcsin(-sqrt(3)/2) + Pik, k прин Z
x = (-1)^(k+1) arcsin(sqrt(3)/2) + Pik, k прин Z
x = (-1)^(k+1) Pi/3 + Pik, k прин Z
===================
2. 2sin^2x - 3sinx + 1 = 0
sinx = t, -1 <= t <= 1
2t^2 - 3t + 1 = 0
D = 9 - 4*2*1 = 1
t1 = (3 + 1)/4 = 1
t2 = (3 - 1)/4 = 1/2
sinx = 1
x = (-1)^k arcsin1 + Pik, k прин Z
x = (-1)^k Pi/2 + Pik, k прин Z
sinx = 1/2
x = (-1)^k arcsin(1/2) + Pik, k прин Z
x = (-1)^k Pi/6 + Pik, k прин Z
===================
6. tg(4x - Pi/6) = -1
4x - Pi/6 = arctg(-1) + Pik, k прин Z
4x - Pi/6 = -arctg(1) + Pik, k прин Z
4x - Pi/6 = -Pi/4+ Pik, k прин Z
4x = -Pi/4 + Pi/6 + Pik, k прин Z
4x = -Pi/12 + Pik, k прин Z
x = -Pi/48 + Pik/4, k прин Z
Похожие вопросы
Предмет: Алгебра,
автор: nimilovicura
Предмет: Русский язык,
автор: kseniaislamova79
Предмет: Химия,
автор: valeriyadibizeva
Предмет: Физика,
автор: Gulnaz19999
Предмет: Информатика,
автор: alenenok4ek