Предмет: Математика,
автор: Esco9
Наидите наибольшее и наименьшее значение функции на отрезке [0;2] .производной f(x)=x^4-4x-2.
Ответы
Автор ответа:
0
решение смотри на фотографии
Приложения:
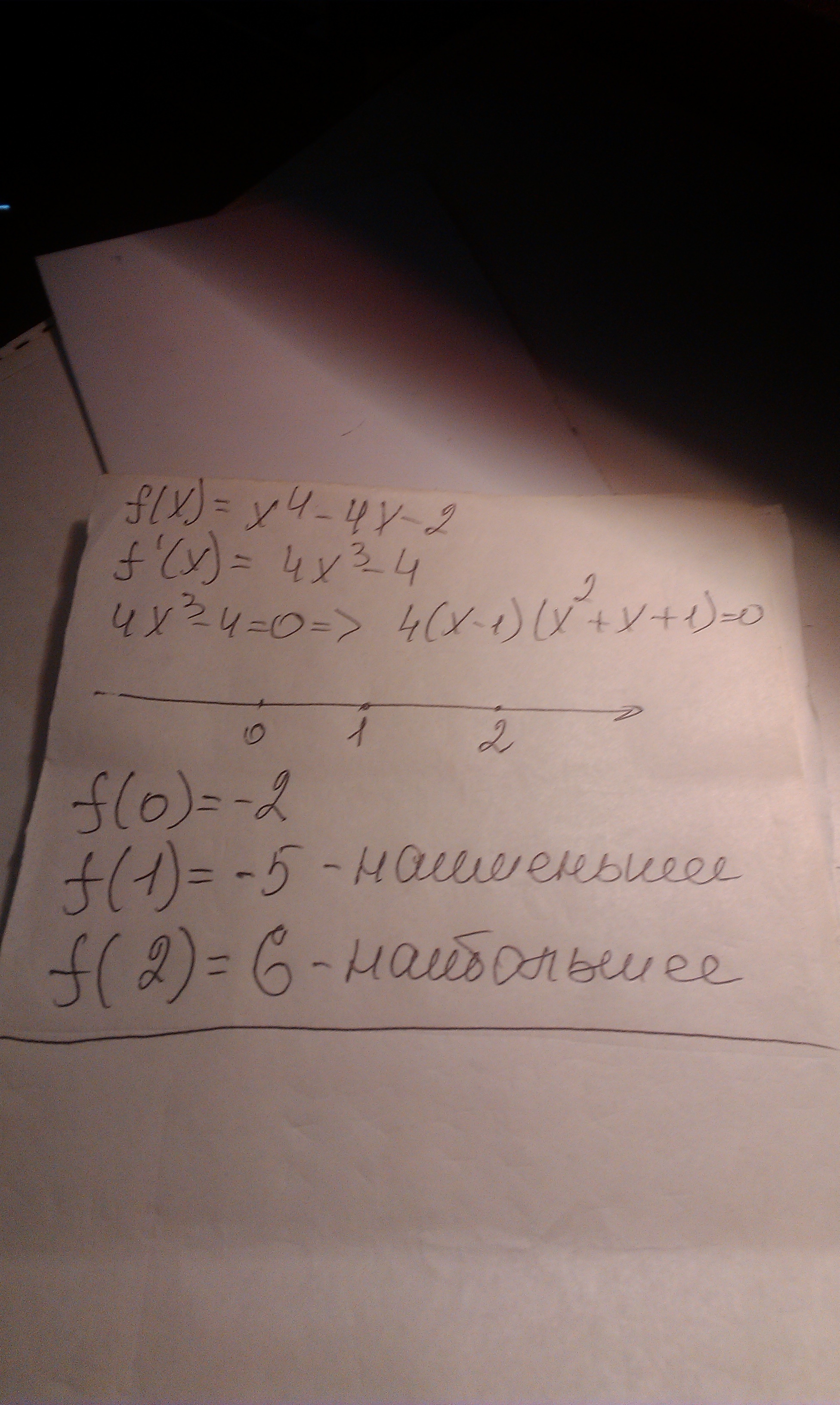
Автор ответа:
0
f(x)=x^4 - 4x - 2
Вычислим значения в критических точках
y' = 4x^3 - 4
4x^3 - 4 = 0
4(x^3 -1) = 0
x^3 - 1 = 0
x^3 = 1
x = 1
f(1) = 1^4 - 4*1 - 2 = 1 - 4 - 2 = -5
Вычислим значения функции на концах отрезка:
f(0) = 0^4 - 4*0 - 2 = -2
f(2) = 2^4 - 4*2 - 2 = 16 - 8 - 2 = 6
Наибольшее значение 6
Наименьшее значение -5
Вычислим значения в критических точках
y' = 4x^3 - 4
4x^3 - 4 = 0
4(x^3 -1) = 0
x^3 - 1 = 0
x^3 = 1
x = 1
f(1) = 1^4 - 4*1 - 2 = 1 - 4 - 2 = -5
Вычислим значения функции на концах отрезка:
f(0) = 0^4 - 4*0 - 2 = -2
f(2) = 2^4 - 4*2 - 2 = 16 - 8 - 2 = 6
Наибольшее значение 6
Наименьшее значение -5
Приложения:
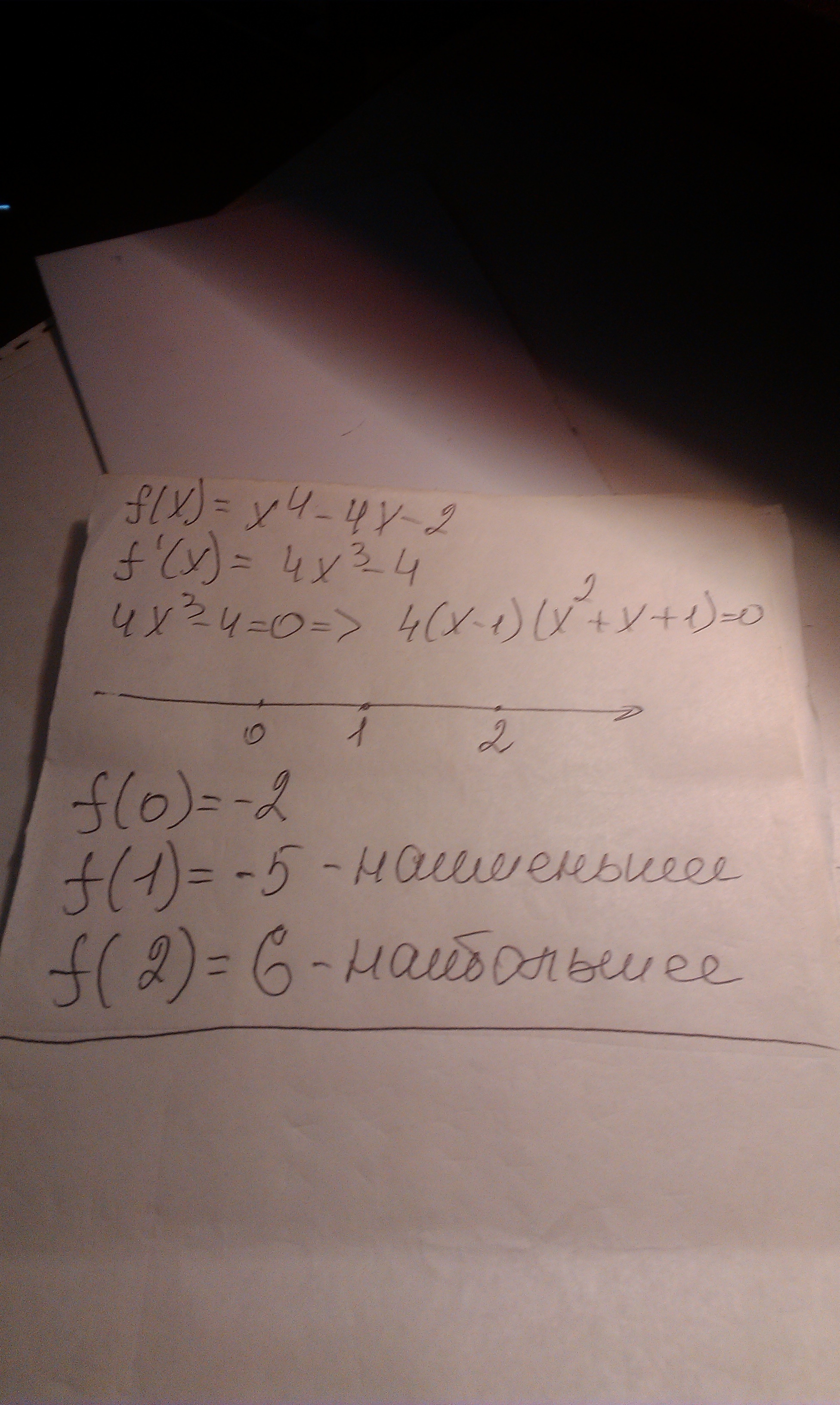
Похожие вопросы
Предмет: История,
автор: irenegrinyuk
Предмет: Химия,
автор: Аноним
Предмет: Русский язык,
автор: futerfur3
Предмет: Литература,
автор: 2222216
Предмет: Литература,
автор: неважнокто15