Предмет: Математика,
автор: Сьюзиss
Помогите,пожалуйста
Общее решение уравнения y'+y=0
Имеет вид :
Варианты ответа ниже на фото
Приложения:
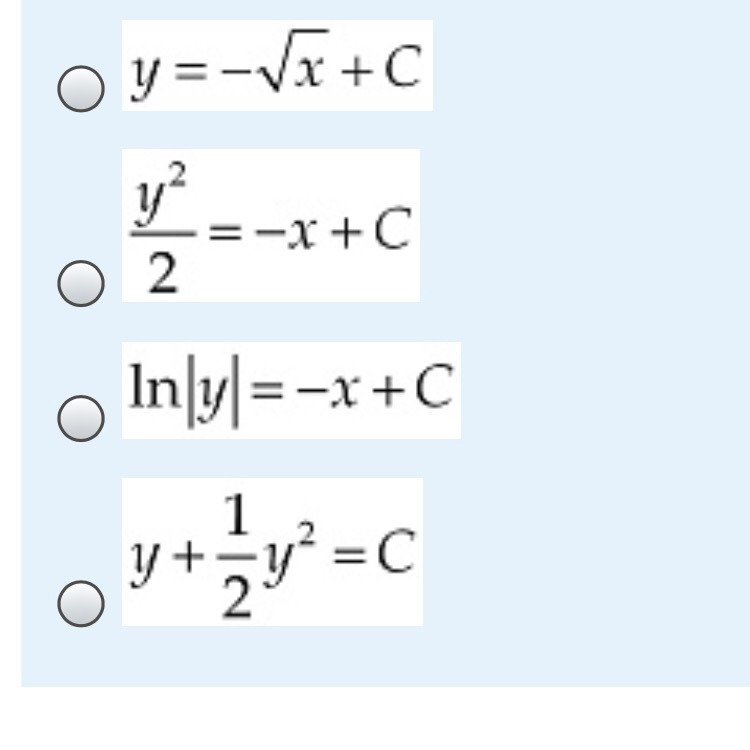
Ответы
Автор ответа:
0
Наше уравнение - линейное однородное с постоянными коэффициентами. Теория рекомендует либо написать характеристическое уравнение, либо разделить переменные. Мы пойдем третьим, более простым путем. Известно, что общее решение такого уравнения - линейного однородного первого порядка - имеет вид
 где
где  какое-нибудь частное ненулевое решение. Угадаем его: из уравнения следует, что
какое-нибудь частное ненулевое решение. Угадаем его: из уравнения следует, что
 то есть при взятии производной функция не меняется, только умножается на - 1. Такому условию удовлетворяет, например,
то есть при взятии производной функция не меняется, только умножается на - 1. Такому условию удовлетворяет, например,
 Поэтому общее решение имеет вид
Поэтому общее решение имеет вид 
Такого ответа нет среди выписанных. Но он почти равносилен третьему. Почти - поскольку там потеряно решение y=0. Поэтому абсолютно правильного ответа среди списка нет.
Такого ответа нет среди выписанных. Но он почти равносилен третьему. Почти - поскольку там потеряно решение y=0. Поэтому абсолютно правильного ответа среди списка нет.
Автор ответа:
0
)))) есть
Автор ответа:
0
Что есть?
Автор ответа:
0
Так ,получается вариант N3?))
Автор ответа:
0
Все,я поняла ))Спасибо ,вам!)
Автор ответа:
0
Но он не совсем полный - y=0 очевидно является решением, но не входит в ответ, записанный в виде логарифма. А происходит это из-за того, что при разделении переменных (в первом способе решения) произошло деление на ноль, в этот момент решение y=0 было потеряно и его нужно отдельно добавлять.
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Литература,
автор: sahmerzaevae
Предмет: Английский язык,
автор: annahappy13
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: elvikarimova