Предмет: Математика,
автор: McMasnik
Нужна помощь с дифф. уравнением
Приложения:
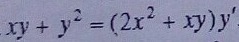
Ответы
Автор ответа:
0
Данное дифференциальное уравнение является однородным. Поэтому производим две замены:
Похожие вопросы
Предмет: История,
автор: daniawady
Предмет: Русский язык,
автор: arinaKotik987
Предмет: Русский язык,
автор: SAMYRAI2703
Предмет: Музыка,
автор: ssaasshhaa11
Предмет: Физика,
автор: Ferbiqt