Предмет: Геометрия,
автор: albinagadaeva1096
Нужно сделать задачу по геометрии
в трапецию с периметром 242 см вписан круг, радиус которого равен 30см.Одна с боковых сторон трапеции делится точкой касания на два равных отрезка. Найдите отрезки второй боковой стороны трапеции, на которые делится точка соприкосновения круга, если их разность равна 11 см
Ответы
Автор ответа:
0
Если в трапецию можно вписать окружность, то суммы ее противоположных сторон равны, значит
AB+CD=BC+AD
По условию периметр трапеции равен 242, следовательно
AB+CD=BC+AD=121
По свойству биссектрис трапеций, прилежащих к ее боковой стороне, AO⊥BO и ΔABO - прямоугольный, а OK - его высота
Пусть AK=KB=x. По свойству высоты прямоугольного треугольника, проведенной к гипотенузе,

значит AB=2*30=60
Решим систему уравнений
CL+LD=121-60
LD-CL=11
2LD=72
LD=36
36-CL=11
CL=25
Ответ: 36см и 25см
AB+CD=BC+AD
По условию периметр трапеции равен 242, следовательно
AB+CD=BC+AD=121
По свойству биссектрис трапеций, прилежащих к ее боковой стороне, AO⊥BO и ΔABO - прямоугольный, а OK - его высота
Пусть AK=KB=x. По свойству высоты прямоугольного треугольника, проведенной к гипотенузе,
значит AB=2*30=60
Решим систему уравнений
CL+LD=121-60
LD-CL=11
2LD=72
LD=36
36-CL=11
CL=25
Ответ: 36см и 25см
Приложения:
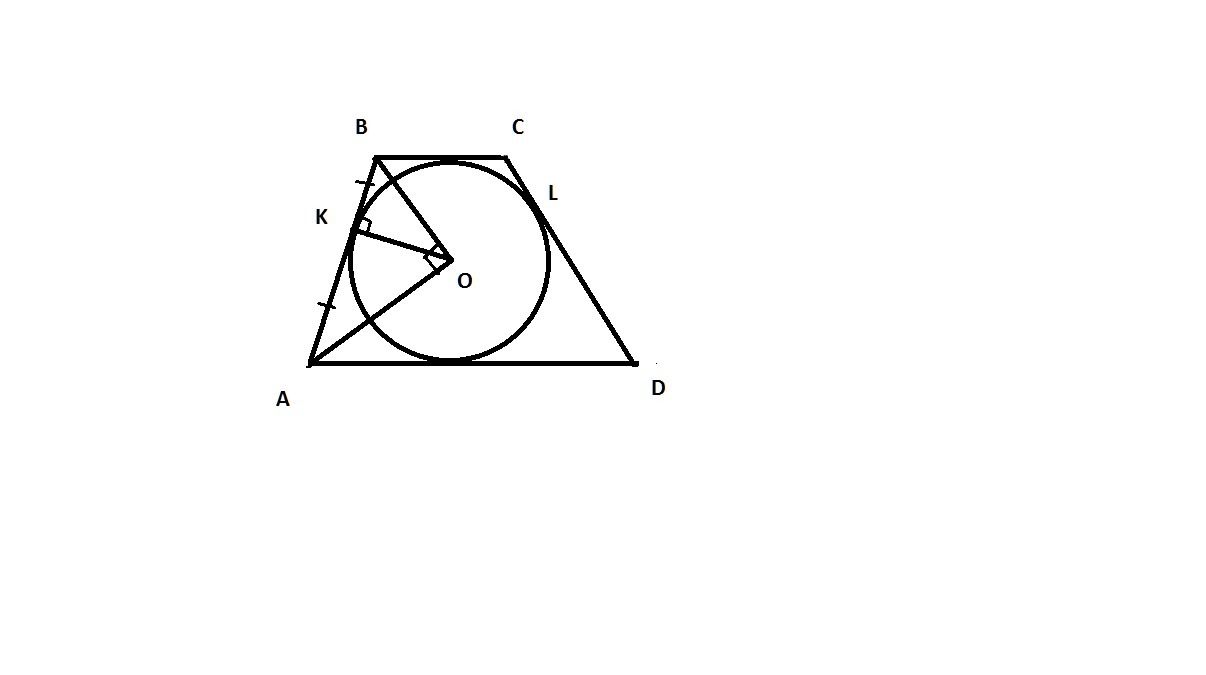
Похожие вопросы
Предмет: Английский язык,
автор: sonyaluck12
Предмет: Английский язык,
автор: kate3235
Предмет: Русский язык,
автор: sjsjjwh
Предмет: Математика,
автор: никсва