Предмет: Математика,
автор: kristinabas19
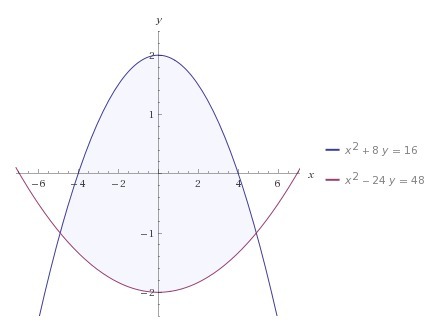
вычислить площадь фигуры ограниченной параболами х^2+8*y=16 и x^2-24*y=48
Ответы
Автор ответа:
0
Находим пределы интегрирования - находим точки пересечение графиков.
Преобразуем уравнения.
1) Y₁ = (16-x²)/8 = - x²/8 + 2
2) Y₂ = (x² - 48)/24 = x²/24 - 2
Находим точки пересечения парабол - пределы интегрирования.
3) Y₂ - Y₁ = 0
(1/24+1/8)*x² = 4
1/6*х² = 4
х² = 24
х = +/- √24 = +/- 2√6 - пределы интегрирования.
Параболы в противоположные стороны, поэтому площадь - сумма площадей каждой.
Формула - интеграл суммы функций - в приложении.
Преобразуем уравнения.
1) Y₁ = (16-x²)/8 = - x²/8 + 2
2) Y₂ = (x² - 48)/24 = x²/24 - 2
Находим точки пересечения парабол - пределы интегрирования.
3) Y₂ - Y₁ = 0
(1/24+1/8)*x² = 4
1/6*х² = 4
х² = 24
х = +/- √24 = +/- 2√6 - пределы интегрирования.
Параболы в противоположные стороны, поэтому площадь - сумма площадей каждой.
Формула - интеграл суммы функций - в приложении.
Приложения:
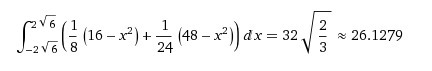
Похожие вопросы
Предмет: История,
автор: vladkabalatskaya228
Предмет: Информатика,
автор: kakushaliza1
Предмет: Другие предметы,
автор: sviridenkotimofej31
Предмет: Русский язык,
автор: KaraS1IK