Предмет: Математика,
автор: Kris9456
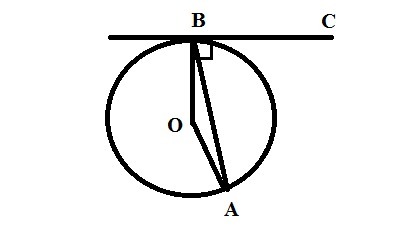
На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Ответы
Автор ответа:
0
Треугольнике OBC равнобедренный (OB=OC - радиус).
Так как углы при основании равны, то ∠OBC=(180°-152°)/2=28°/2=14°.
Радиус OB и касательная BC перпендикулярны, т. е. ∠OBC=90°. Тогда ∠ABC=∠OBC-∠OBA=90°-14°=76°.
Так как углы при основании равны, то ∠OBC=(180°-152°)/2=28°/2=14°.
Радиус OB и касательная BC перпендикулярны, т. е. ∠OBC=90°. Тогда ∠ABC=∠OBC-∠OBA=90°-14°=76°.
Приложения:
Похожие вопросы
Предмет: Физкультура и спорт,
автор: msrd
Предмет: Алгебра,
автор: 4inchopa
Предмет: Математика,
автор: lerakorshunova90
Предмет: Математика,
автор: poyarkovak1
Предмет: География,
автор: Аноним