Предмет: Математика,
автор: darikadasha
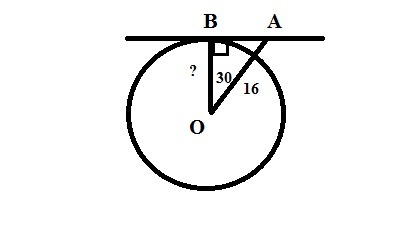
Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите радиус окружности, если угол АОВ = 30°, ОА=16 см
Ответы
Автор ответа:
0
Так радиус OB перпендикулярен касательной AB, то треугольник ABC - прямоугольный.

Приложения:
Похожие вопросы
Предмет: История,
автор: nikkelvarvara
Предмет: Геометрия,
автор: madrahimovazilola0
Предмет: Кыргыз тили,
автор: ekaterinarubilina08
Предмет: Математика,
автор: pyparka