Question

Найдите углы параллелограмма, если один из них на 32 градуса меньше другого

Answer 1

Ответ:

∠A=∠C=74°, ∠B=∠D=106°

Объяснение:

Дано:

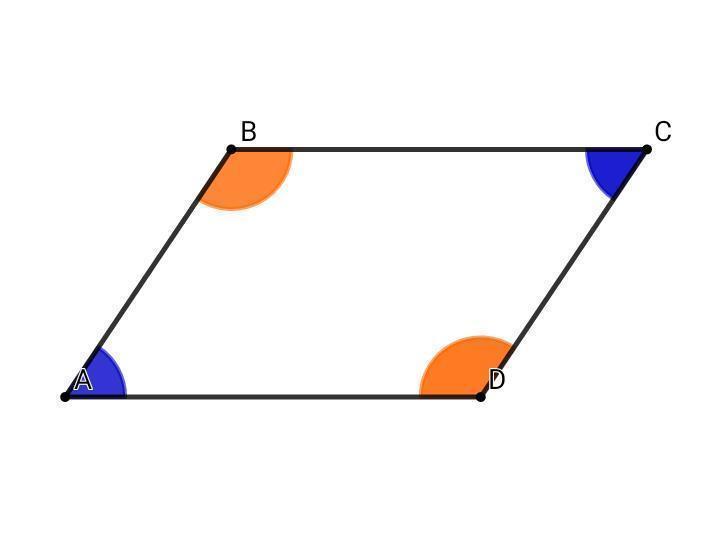
Параллелограмм ABCD (см. рисунок)

Один угол меньше на 32° другого

Найти: ∠A, ∠B, ∠C, ∠D

Решение.

По свойству параллелограмма противоположные углы параллелограмма попарно равны и поэтому ∠A=∠C и ∠B=∠D. В силу этого (см. рисунок) можем предположит, что ∠A=∠B-32°. Так как соседние углы ∠A и ∠B смежные, то ∠A+∠B=180°. Подставляем выражение для угла ∠A в последнее равенство:

∠B-32°+∠B=180°

2·∠B=180°+32°

2·∠B=212°

∠B=106°

Тогда: ∠C=∠A=106°-32°=74°, ∠D=∠B=106°.

Answer 2

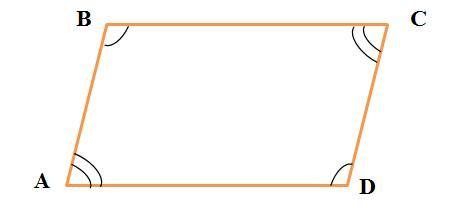
• Параллелограмм - это четырёхугольник, у которого противолежащие стороны попарно параллельны, и углы попарно равны

Пусть острый угол параллелограмма ∠А = ∠С = х, тогда

∠В = ∠D = x + 32°. Сумма всех углов в четырёхугольнике равна 360°, тогда составляем уравнение:

х + х + (х + 32°) + (х + 32°) = 360°

4х = 296°   ⇒    х = 74°

Значит, ∠А = ∠С = 74° , ∠В = ∠D = 74° + 32° = 106°

Ответ: 74° , 106° , 74° , 106°.