Предмет: Математика,
автор: Algerd
Решите неравенство!!
Приложения:
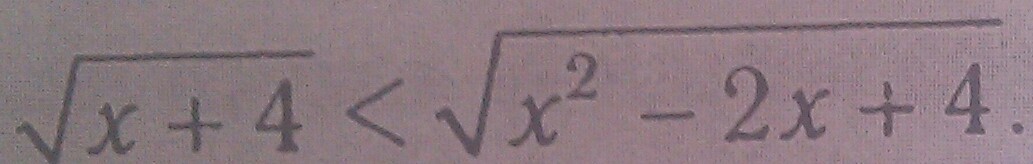
Ответы
Автор ответа:
0
√(x+4)<√(x²-2x+4) - возведем неравенство во вторую степень
x+4<x²-2x+4
x²-2x+4>x+4
x²-3x>0
х(х-3)>0
это неравенство расписывается на две группы неравенств
первая группа неравенств
х>0 -> хє(0;+оо)
х-3>0 -> х>3 -> хє(3;+оо)
общая область - пересечение найденных областей -> хє(3;+оо)
вторая группа неравенств
х<0 -> хє(-оо;0)
х-3<0 -> х<3 -> хє(-оо;3)
общая область - пересечение найденных областей -> хє(-оо;0)
область, удовлетворяющая неравенству х(х-3)>0 - обьединение областей, найденных при решении двух групп неравенств -> хє(-оо;0)U(3;+оо)
ОДЗ функции √(x+4)
x+4≥0 -> x≥-4 -> xє[-4;+oo)
ОДЗ функции √(x²-2x+4)
(x²-2x+4)≥0
решим уравнение
(x²-2x+4)=0
дискриминант
D=(-2)² - 4*1*(-4) = 4+16=20
√D=√20=√(4*5)=2√5
первое неизвестное
x=(-(-2)+2√5)/(2*1)=(2+2√5)/2= 1+√5
второе неизвестное
x=(-(-2)-2√5)/(2*1)=(2-2√5)/2= 1-√5
(x²-2x+4)≥0 -> (х-(1+√5))(х-(1-√5))≥0
это неравенство расписывается на две группы неравенств
первая группа неравенств
х-(1+√5)≥0 -> х≥1+√5 -> хє[1+√5;+оо)
х-(1-√5)≥0 -> х≥1-√5 -> хє[1-√5;+оо)
общая область - пересечение найденных областей -> хє[1+√5;+оо)
вторая группа неравенств
х-(1+√5)≤0 -> х≤1+√5 -> хє(-оо;1+√5]
х-(1-√5)≤0 -> х≤1-√5 -> хє(-оо;1-√5]
общая область - пересечение найденных областей -> хє(-оо;1-√5]
область, удовлетворяющая неравенству (x²-2x+4)≥0 - обьединение областей, найденных при решении двух групп неравенств -> хє(-оо;1-√5]U[1+√5;+оо)
область, удовлетворяющая неравенству
√(x+4)<√(x²-2x+4) - пересечение области, удовлетворяющей неравенству х(х-3)>0 и ОДЗ функций, составляющих начальное неравенство √(x+4)<√(x²-2x+4)
Выпишем области, которые нужно пересечь
хє(-оо;0)U(3;+оо)
xє[-4;+oo)
хє(-оо;1-√5]U[1+√5;+оо)
1-√5 ≈ 1-2,4=-1,4
1+√5 ≈ 1+2,4=3,4
Пересечением областей будет следующая область
хє[-4;1-√5]U[1+√5;+оо) - область, удовлетворяющая начальному неравенству
x+4<x²-2x+4
x²-2x+4>x+4
x²-3x>0
х(х-3)>0
это неравенство расписывается на две группы неравенств
первая группа неравенств
х>0 -> хє(0;+оо)
х-3>0 -> х>3 -> хє(3;+оо)
общая область - пересечение найденных областей -> хє(3;+оо)
вторая группа неравенств
х<0 -> хє(-оо;0)
х-3<0 -> х<3 -> хє(-оо;3)
общая область - пересечение найденных областей -> хє(-оо;0)
область, удовлетворяющая неравенству х(х-3)>0 - обьединение областей, найденных при решении двух групп неравенств -> хє(-оо;0)U(3;+оо)
ОДЗ функции √(x+4)
x+4≥0 -> x≥-4 -> xє[-4;+oo)
ОДЗ функции √(x²-2x+4)
(x²-2x+4)≥0
решим уравнение
(x²-2x+4)=0
дискриминант
D=(-2)² - 4*1*(-4) = 4+16=20
√D=√20=√(4*5)=2√5
первое неизвестное
x=(-(-2)+2√5)/(2*1)=(2+2√5)/2= 1+√5
второе неизвестное
x=(-(-2)-2√5)/(2*1)=(2-2√5)/2= 1-√5
(x²-2x+4)≥0 -> (х-(1+√5))(х-(1-√5))≥0
это неравенство расписывается на две группы неравенств
первая группа неравенств
х-(1+√5)≥0 -> х≥1+√5 -> хє[1+√5;+оо)
х-(1-√5)≥0 -> х≥1-√5 -> хє[1-√5;+оо)
общая область - пересечение найденных областей -> хє[1+√5;+оо)
вторая группа неравенств
х-(1+√5)≤0 -> х≤1+√5 -> хє(-оо;1+√5]
х-(1-√5)≤0 -> х≤1-√5 -> хє(-оо;1-√5]
общая область - пересечение найденных областей -> хє(-оо;1-√5]
область, удовлетворяющая неравенству (x²-2x+4)≥0 - обьединение областей, найденных при решении двух групп неравенств -> хє(-оо;1-√5]U[1+√5;+оо)
область, удовлетворяющая неравенству
√(x+4)<√(x²-2x+4) - пересечение области, удовлетворяющей неравенству х(х-3)>0 и ОДЗ функций, составляющих начальное неравенство √(x+4)<√(x²-2x+4)
Выпишем области, которые нужно пересечь
хє(-оо;0)U(3;+оо)
xє[-4;+oo)
хє(-оо;1-√5]U[1+√5;+оо)
1-√5 ≈ 1-2,4=-1,4
1+√5 ≈ 1+2,4=3,4
Пересечением областей будет следующая область
хє[-4;1-√5]U[1+√5;+оо) - область, удовлетворяющая начальному неравенству
Похожие вопросы
Предмет: История,
автор: vlad382284
Предмет: Математика,
автор: mukhtararovasabina
Предмет: Геометрия,
автор: kostrix61
Предмет: Биология,
автор: asd149